Paper Notes: Attention Is All You Need

Notes on this classic masterpiece: Attention is All You Need.

Attention is All You Need

• Published at NeurIPS 2017, cited 170K+ times.
• Contribution: Originally applied to translation tasks, later widely extended to non-NLP fields.
• Main innovations:
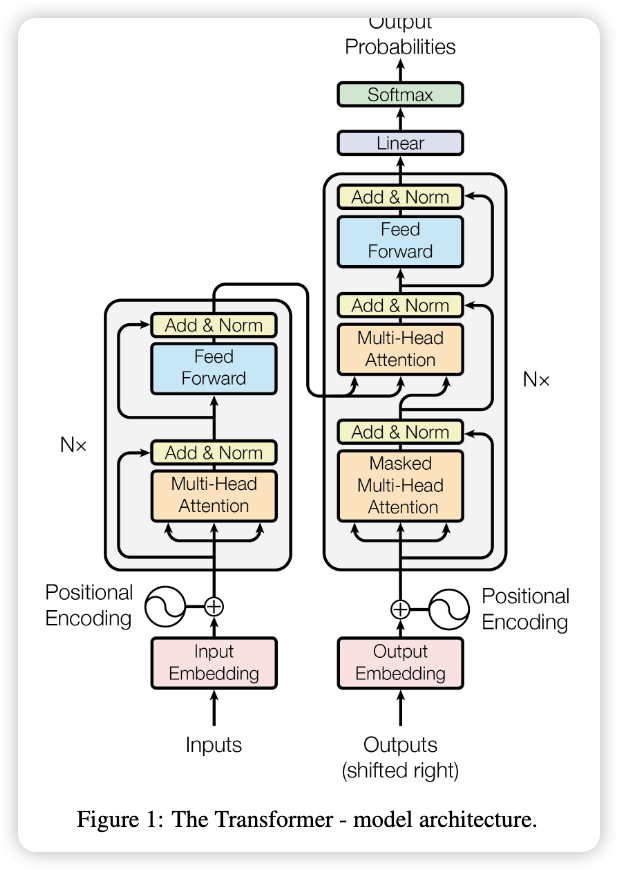
  • Transformer architecture
  • Multi-head attention mechanism
  • Encoder and Decoder

Background

• Word2vec:

  • Embedding:

    The goal of text representation is to transform unstructured data into structured data. There are three basic methods:

    1. One-hot representation: one word, one bit
    2. Integer encoding
    3. Word embedding: vector encoding, with three main advantages:
       (1) Uses low-dimensional vectors instead of long one-hot/character representations;
       (2) Words with similar semantics are closer in vector space;
       (3) Versatile across tasks.

  • Two mainstream embedding methods: Word2vec and GloVe.

  • Word2vec: A statistical method for learning word vectors. Proposed by Mikolov at Google in 2013.
    https://easyai.tech/en/ai-definition/word2vec/

    It has two training modes:

    • Predict current word from context
    • Predict context from current word

  • GloVe extends Word2vec by combining global statistics with context-based learning.

  • Difference from tokenizer (e.g., SentencePiece):

    Item	Tokenizer	Word2Vec
    Function	Splits text into words	Converts words into vectors
    Order	First: generate word list	Then: train embeddings
    Necessity	Word2Vec requires explicit word units, so depends on tokenizer (especially in Chinese)

Methods

Embedding

• Input embedding: transforms natural language into vectors. The paper uses Word2vec.

• Positional embedding: two approaches

  1. trainable like input embedding;
  2. function-based.

  Formula (dimension matches input embedding, $pos$ = position, $i$ = dimension index):

  $$\begin{aligned} PE_{(pos,2i)} &= \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) \\ PE_{(pos,2i+1)} &= \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) \end{aligned}$$

  Question	Answer
  Is sin/cos just for convenience?	❌ No, they have mathematical motivation
  Why sin for 2i, cos for 2i+1?	To introduce phase shift and complementarity
  Advantages?	Orthogonality, phase info, multi-frequency composition, relative position inference

  Mathematical property: $PE_{(pos,2i)}^2 + PE_{(pos,2i+1)}^2 = 1$

  Benefits:
  a) Works for unseen longer sequences;
  b) Supports relative position inference.

  Differences across dimensions:
  

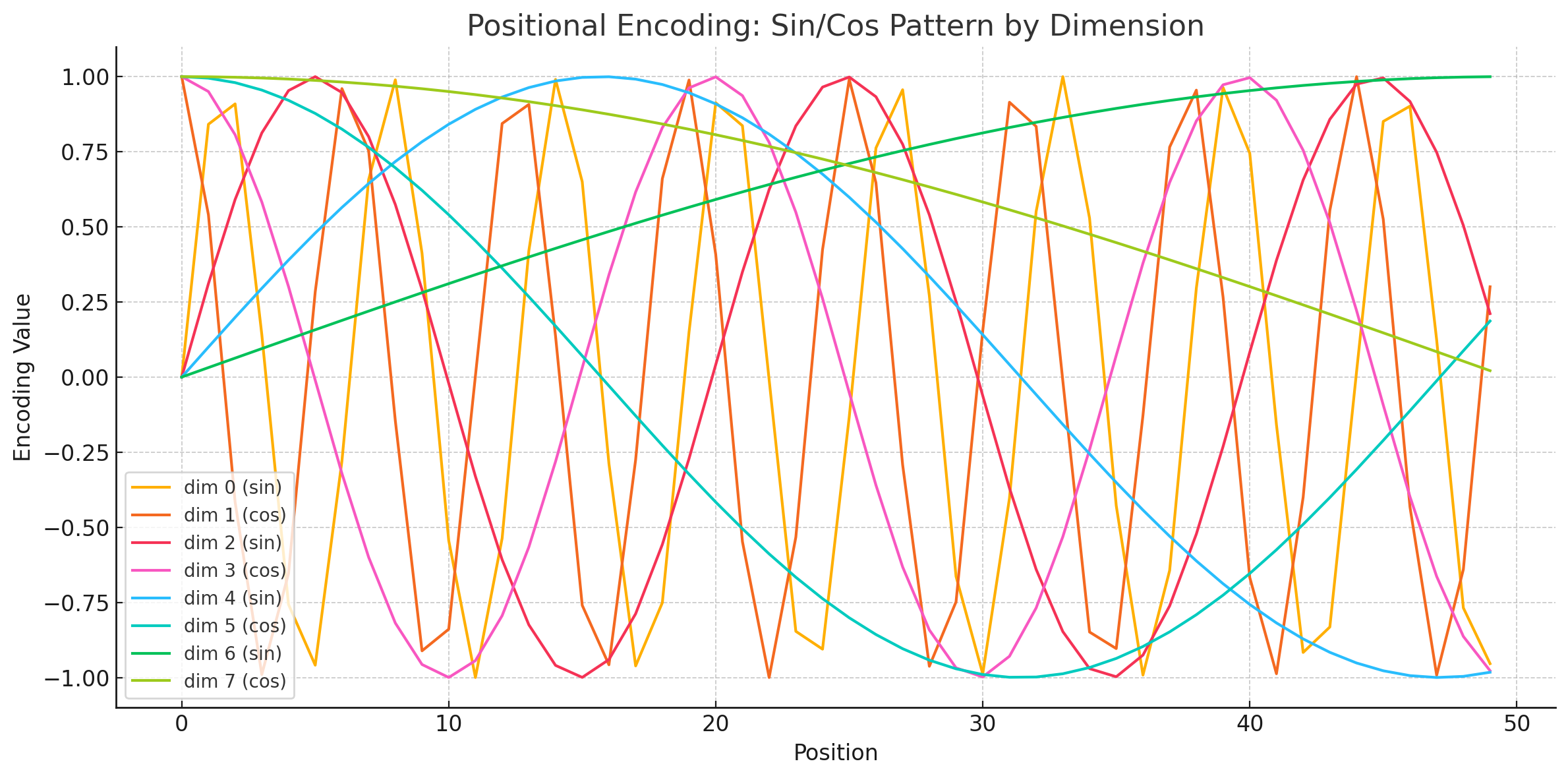
• Final input:

  $$X = Input + Positional$$

Self-Attention

The four words “with power and sum” can be highly summarized

• Core idea: “From paying attention to everything to focusing on what matters.”

• First used in computer vision, later popularized in NLP, especially after BERT and GPT (2018). Transformers and attention became the core focus.

• Three advantages: fewer parameters, faster, better performance.

• Solves RNN’s problem of sequential dependency. Attention allows:

  • Process all inputs at once
  • Compute pairwise dependencies in parallel
  • Preserve long-range dependencies

• Example:

  Input: "The cat sat on the mat"

  To compute "The" representation:

  Word	Attention score
  The	0.1
  cat	0.3
  sat	0.2
  on	0.1
  the	0.1
  mat	0.2

  Weighted sum of vectors gives new "The" representation.
  ⚠️ All words’ attention can be computed simultaneously!

• Principle:

  

  General form:

  $$Attention(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$$

  $Q,K,V$ are derived from input $X$ via linear projections.

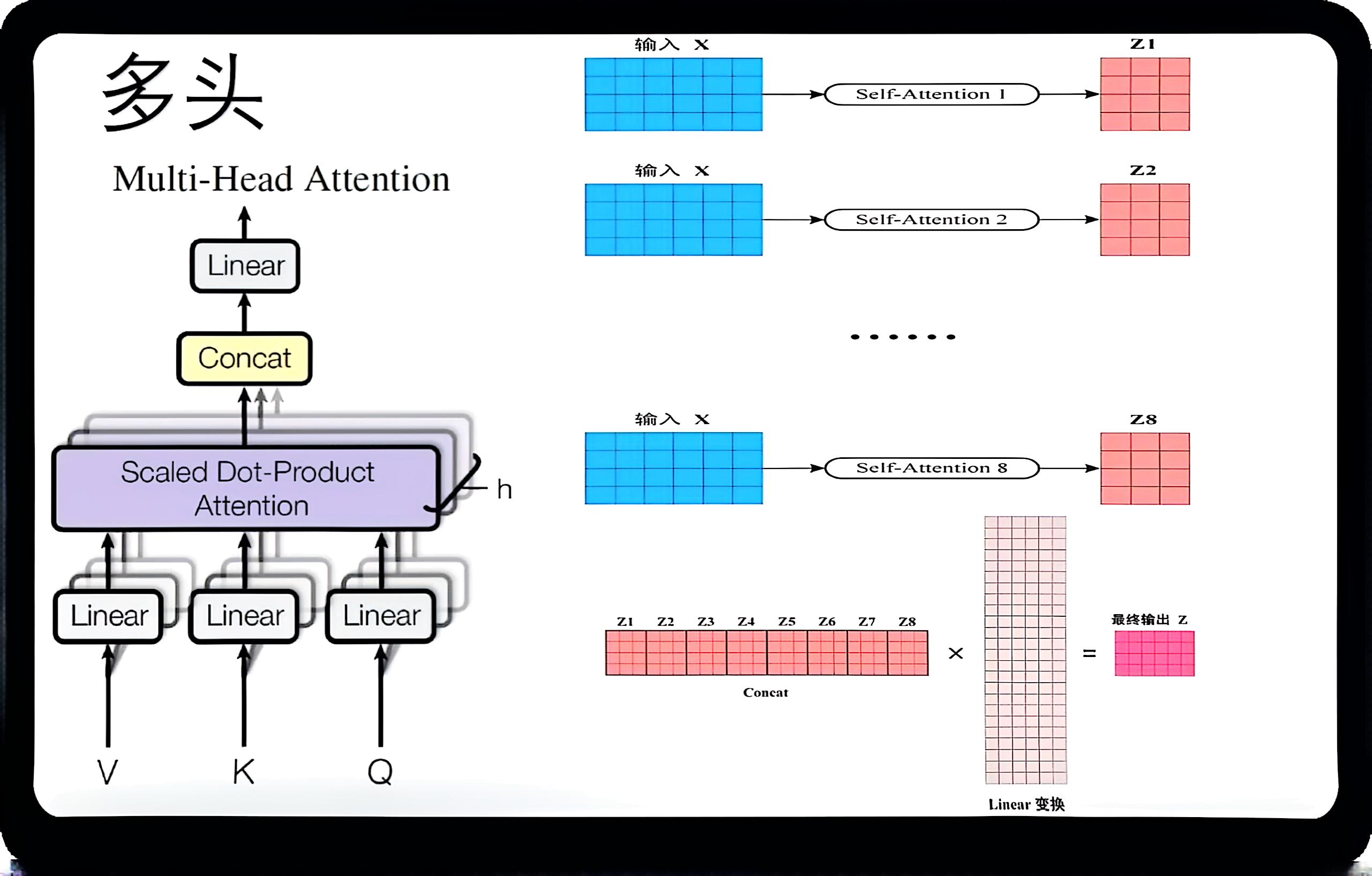
  • Multi-head attention:

    $$\begin{aligned} MultiHead(Q,K,V) &= Concat(head_1,...,head_h)W^O \\ head_i &= Attention(QW_i^Q, KW_i^K, VW_i^V) \end{aligned}$$

    Advantages:

    • Each head focuses on different aspects (positions/features).
    • Stronger representational power.
    • Analogy: multiple perspectives while reading a text (relations, timeline, causality).

    

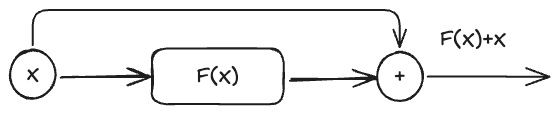
Add & Norm

• Add = residual connection (helps training deeper networks):

  $$Add = X + MultiHead(X)$$

  

• Norm = Layer Normalization (normalize to zero mean, unit variance → faster convergence).

Feed Forward

• Two layers: ReLU + linear output

  $$FFN(x) = \max(0, xW_1+b_1)W_2+b_2$$

• Same transformation applied independently to each position, but parameters differ across layers.

  Component	Meaning
  FFN	Two fully connected layers + ReLU (expand then reduce)
  Usage	Per-position, parameter-shared
  Parameters	Different per-layer
  Optimization	Equivalent to two 1x1 convolutions
  Dimensions	Input/output 512, hidden 2048

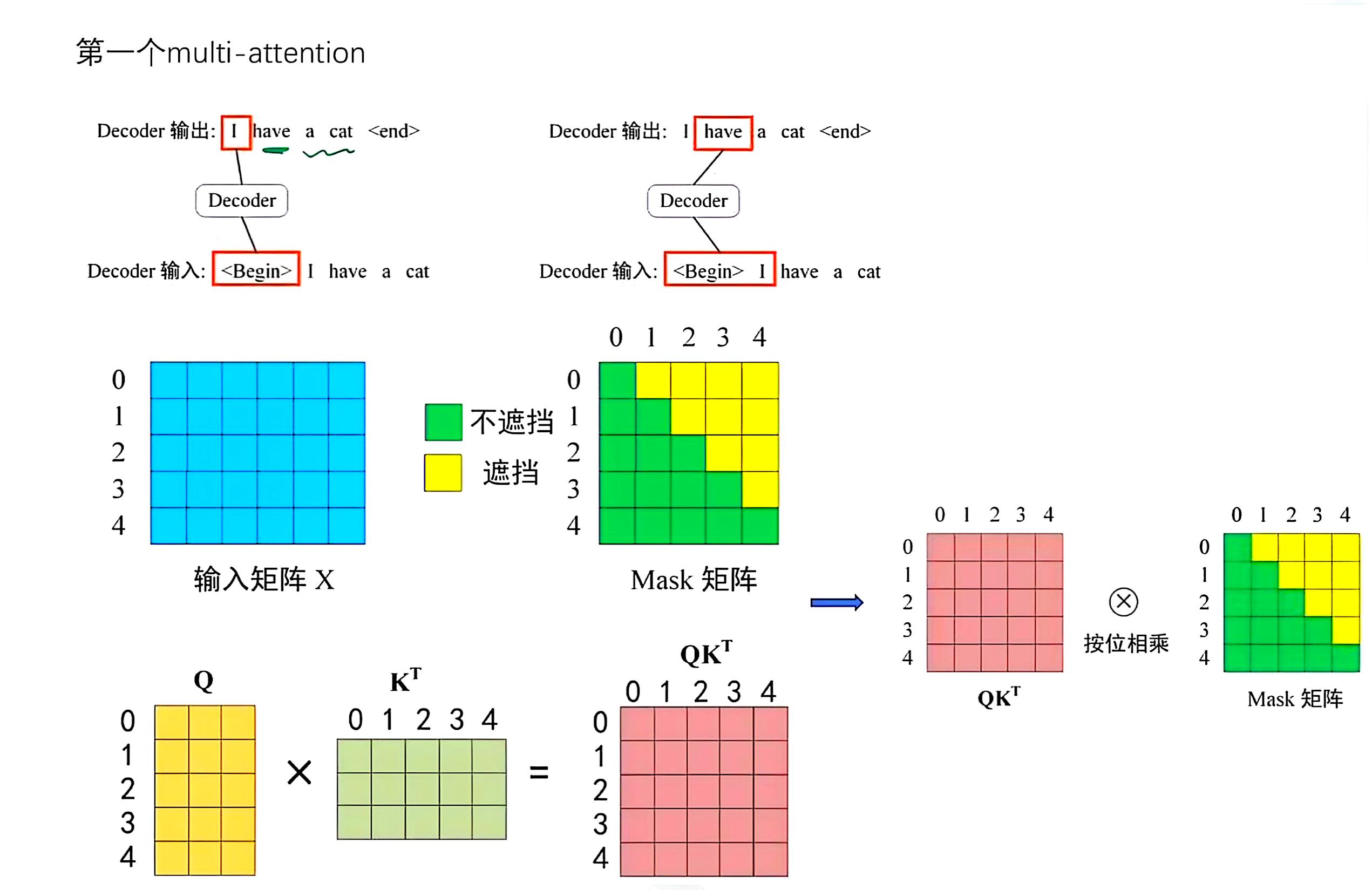
Mask

• Before multi-head attention in decoder, a mask is applied.

• Purpose: Translation is sequential — cannot see future tokens.
  

  $$Attention(Q, K, V) = \text{softmax}\left(\frac{QK^TM}{\sqrt{d_k}}\right)V$$

  

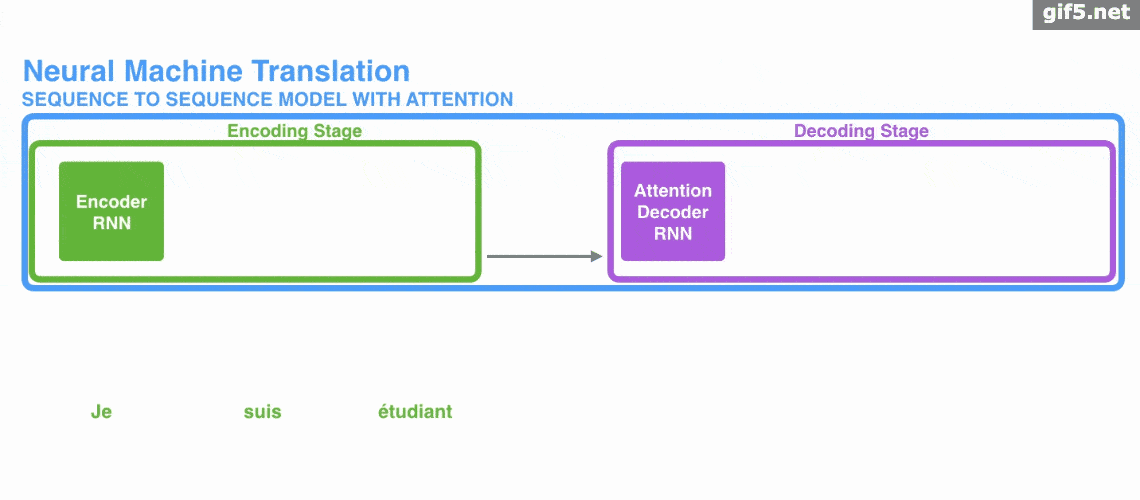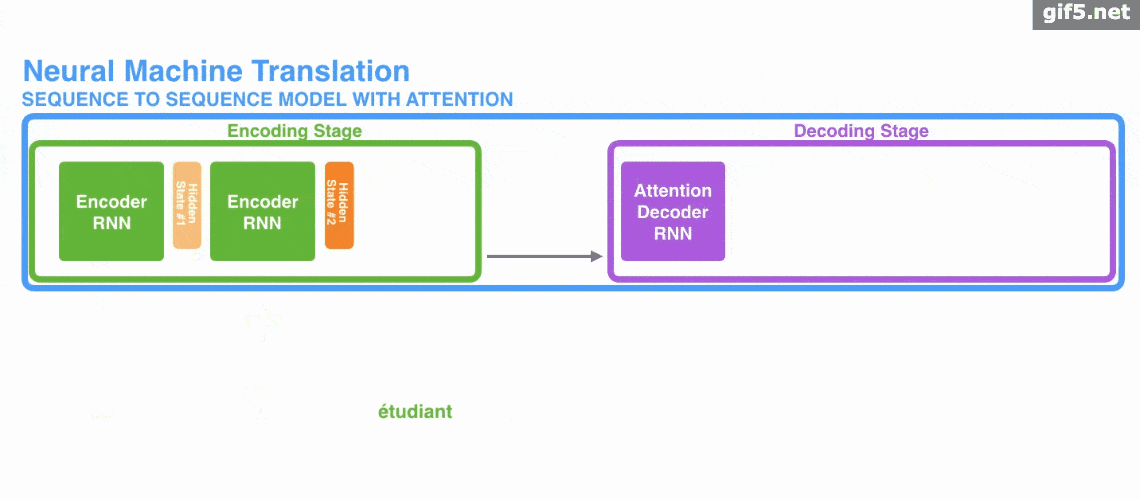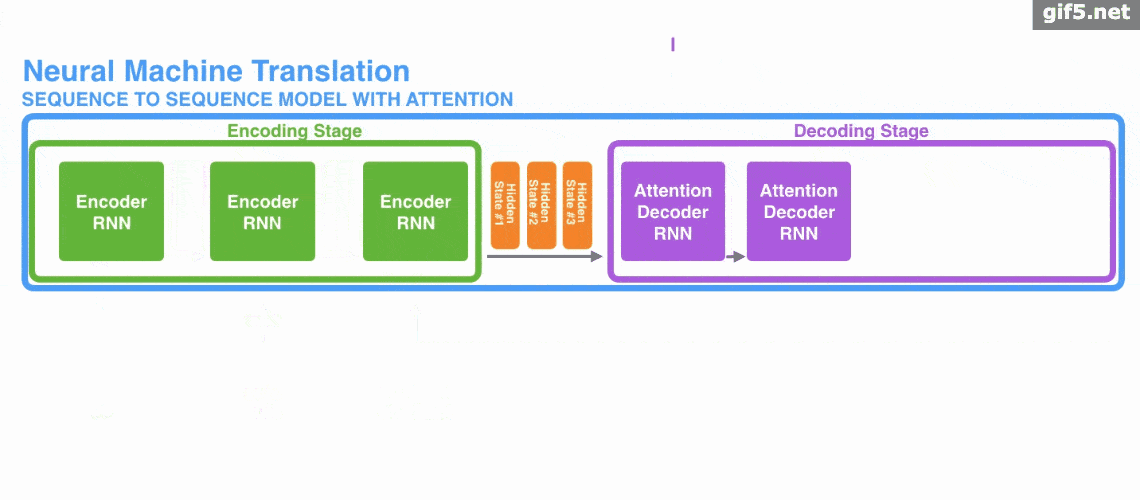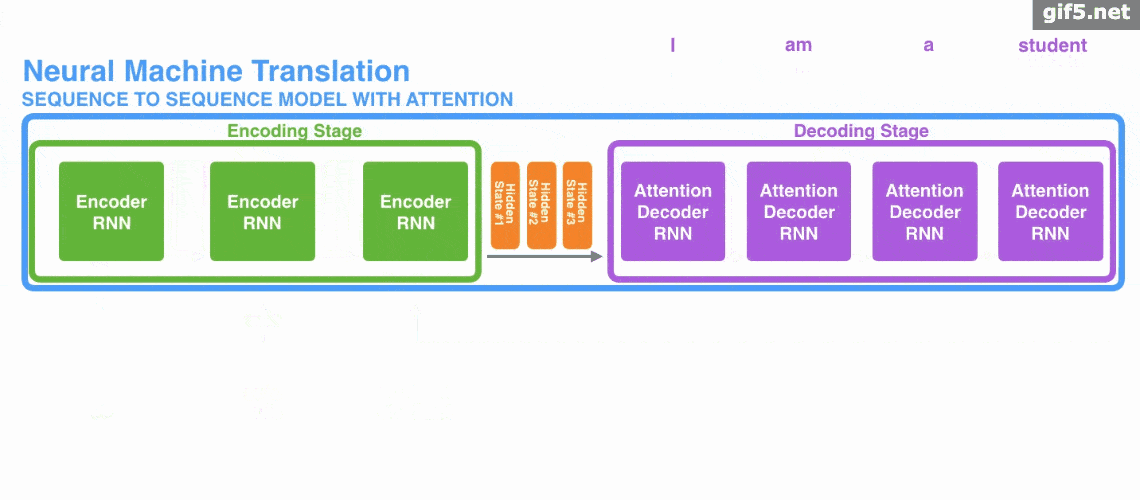
Decoder Structure

• Takes two inputs: previous outputs + current input.
• $K,V$ come from encoder output; $Q$ comes from decoder’s first sublayer.

---

References

• Beginner-friendly transformer explanation
• Attention mechanism
• Vaswani, Ashish, et al. “Attention is all you need.” NeurIPS 2017