Paper Notes: Low-Rank Adaptation of Large Language Models

LoRA is a lightweight fine-tuning technique for large models.

Introduction to LoRA

  • Authors: $Edward Hu^* , Yelong Shen^*$ et al.

  • Publication time: October 16, 2021

  • Motivation: Full-parameter fine-tuning of large models has become impractical.

  • Idea: Low-Rank Adaptation (LoRA)

    1. Freeze pretrained model parameters: Keep weights learned during pretraining unchanged, no further updates.
    2. Insert trainable matrices in each Transformer layer: These are low-rank decomposition matrices with much fewer parameters.
    3. Goal: For downstream tasks (classification, QA, translation, etc.), train only the small added matrices instead of the entire model.
    4. Benefit: Greatly reduces trainable parameter count, saving compute and memory while maintaining performance.

    LoRA illustration

  • Advantages:

    1. Lightweight, plugin-style fine-tuning method
    2. Efficient task switching by swapping small modules, not the whole model
    3. Faster training, less GPU memory, quicker deployment
    4. Compatible with other fine-tuning methods

What is Low-Rank?

✅ 1. Intuition

Neural networks often use large linear transformation matrices (e.g., fully connected layers). For example:
$W \in \mathbb{R}^{d \times k}$ has $d^2$ parameters.

A low-rank matrix approximates $W$ using the product of two smaller matrices:

Wapprox=A⋅B W_{\text{approx}} = A \cdot B
  • $A \in \mathbb{R}^{d \times r}$
  • $B \in \mathbb{R}^{r \times k}$
  • $r \ll \min(d,k)$ (the rank)

✅ 2. LoRA Perspective

In a Transformer, a typical linear transformation is:

y=Wx y = W x

LoRA modifies it as:

  • Keep the original $W$ frozen
  • Add a trainable low-rank term: y=Wx+ΔWx,ΔW=A⋅B y = W x + \Delta W x, \quad \Delta W = A \cdot B

So LoRA adjusts the output with a small trainable low-rank matrix, without touching the main parameters.

✅ 3. Why Low-Rank?

  • Efficient: Few trainable parameters
  • Less prone to overfitting: Simpler, more stable
  • Flexible: Proven effective in modifying model outputs despite low rank

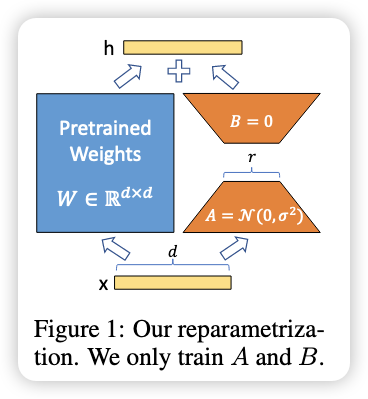
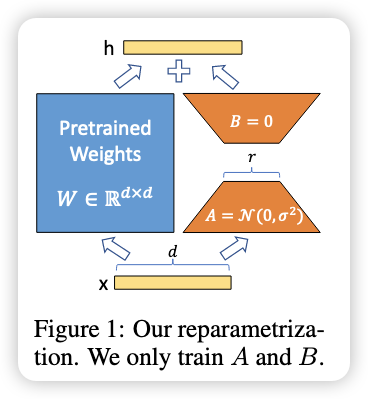
Method

  • Weight formula:

    h=W0x+ΔWx=W0x+BAx h = W_0 x + \Delta W x = W_0 x + B A x

    LoRA math

  • Initialization:

    Item Meaning
    A initialization Random normal distribution (standard init)
    B initialization All zeros (initial extra output = 0)
    Output scaling Scale $\Delta W x$ as $\frac{\alpha}{r} \Delta W x$ to control influence
    Purpose Prevents too strong/weak effect, simplifies hyperparameter tuning
    Practical tip Simply set $\alpha = r$. Adjusting $\alpha$ ≈ adjusting learning rate.

  • Code: https://github.com/microsoft/LoRA

References

DeepLearningLLM