Deep Learning: What Is Regularisation ?

Categories and Comparison of Regularization Methods

1. What is Regularization

(Source: Gpt-4o mini)

Regularization is a technique to prevent overfitting, mainly used in machine learning and statistical modeling. Overfitting happens when a model learns the training data too well, capturing noise instead of underlying patterns, resulting in poor performance on new data.

Core idea of regularization:

  • Penalize complex models: Add an extra penalty term (regularization term) to the loss function to constrain model complexity. This encourages optimization to consider both prediction accuracy and model simplicity.

Benefits of regularization:

  • Improve generalization: Reduce model complexity to achieve more stable performance on unseen data.
  • Feature selection: L1 regularization can set some feature weights to zero.
  • Control overfitting: Prevent the model from learning noise in training data, improving predictive ability.

2. Why Regularize

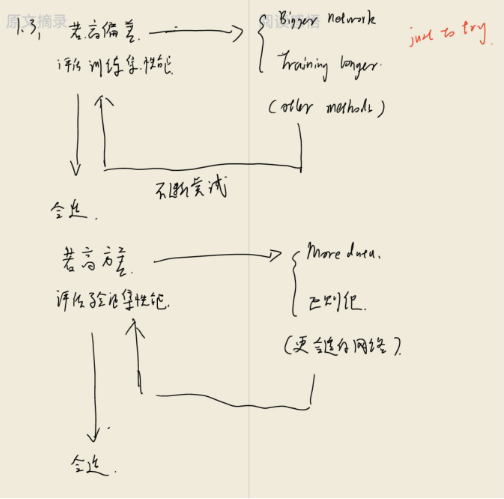
Overfitting vs Underfitting

(My notes)

  • Training a model is a long and iterative process. When fitting data, we usually encounter: overfitting, underfitting, and just-right fitting—corresponding to high variance, high bias, and ideal fit.
  • To reduce high variance (overfitting), three common approaches exist:
    1. Clean the data (time-consuming)
    2. Reduce model parameters and complexity
    3. Add a penalty factor, i.e., regularization

For a regression model:

hθ(x)=θ0+θ1x1+θ2x22+θ3x33+θ4x44 h_{\theta}(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2^2 + \theta_3 x_3^3 + \theta_4 x_4^4 J(θ)=1m∑i=1m(hθ(x(i))−y(i))2 J(\theta) = \frac{1}{m} \sum_{i=1}^m (h_{\theta}(x^{(i)}) - y^{(i)})^2

Higher-order terms make the model more flexible, increasing variance. Limiting these coefficients (e.g., $\theta_3, \theta_4$) helps reduce overfitting:

min⁡θJ(θ)=12m[∑i=1m(hθ(x(i))−y(i))2+1000θ32+10000θ42] \min_\theta J(\theta) = \frac{1}{2m} \left[ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 + 1000 \theta_3^2 + 10000 \theta_4^2 \right]

3. How to Regularize Models

  • Introduce three common methods:
    • $L_2$ Regularization
    • $L_1$ Regularization
    • Dropout

3.1 $L_2$ Parameter Regularization (Frobenius Norm)

Also known as Ridge Regression or Tikhonov Regularization.

  • Method: Add a regularization term to the objective function:

    J(θ)=1m∑i=1m(hθ(x(i))−y(i))2+λ∑j=1nθj2 J(\theta) = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2 + \lambda \sum_{j=1}^{n} \theta_j^2

  • For logistic regression:

J(w,b)=1m∑i=1m(y^(i),y(i))+λ2m∣∣w∣∣22 J(w,b) = \frac{1}{m} \sum_{i=1}^{m} (\hat{y}^{(i)}, y^{(i)}) + \frac{\lambda}{2m} ||\mathbf{w}||_2^2

  • $\mathbf{w} = [w_1, w_2, …, w_n]$ is the weight vector (excluding bias). The regularization term penalizes large weights to prevent overfitting.

  • $||\mathbf{w}||_2^2 = w_1^2 + w_2^2 + … + w_n^2$

  • $\frac{\lambda}{2m}$ scales the regularization effect relative to dataset size.

Why $L_2$ works:

  • Adds $\Omega(\theta) = \frac{1}{2m} ||\mathbf{w}||_2^2$ to the loss, affecting backpropagation.
  • Weight update effectively performs weight decay, shrinking all weights proportionally.

L2 Illustration Weight Decay

3.2 $L_1$ Regularization

  • In linear regression, called Lasso Regression:
Ω(θ)=∣∣w∣∣1=∑i∣wi∣ \Omega(\theta) = ||\mathbf{w}||_1 = \sum_i |w_i|
  • Sparsity: Many parameters become zero, achieving feature selection—important in high-dimensional tasks like NLP or genomics.
  • L1 can also reduce overfitting, though its primary use is sparsity.

Reference: Deep Understanding of L1/L2 Regularization

3.3 Dropout (Random Deactivation)

  • Common in CV and deep learning.

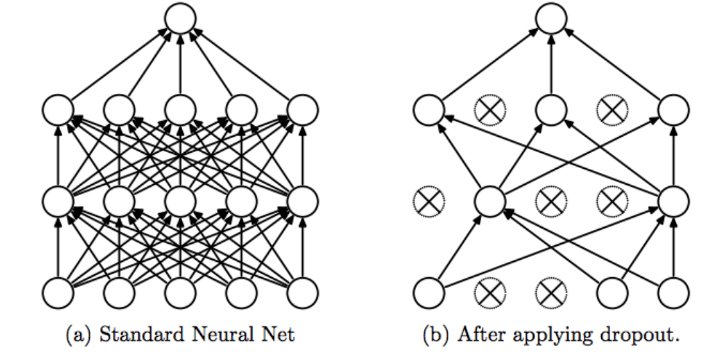
Dropout Illustration

  • Randomly remove neurons during training to reduce overfitting.
  • Inverted Dropout: scale activations by keep probability to maintain expected value:
d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep_prop
a3 = a3 * d3
a3 /= keep_prop
DeepLearningmathRegularization