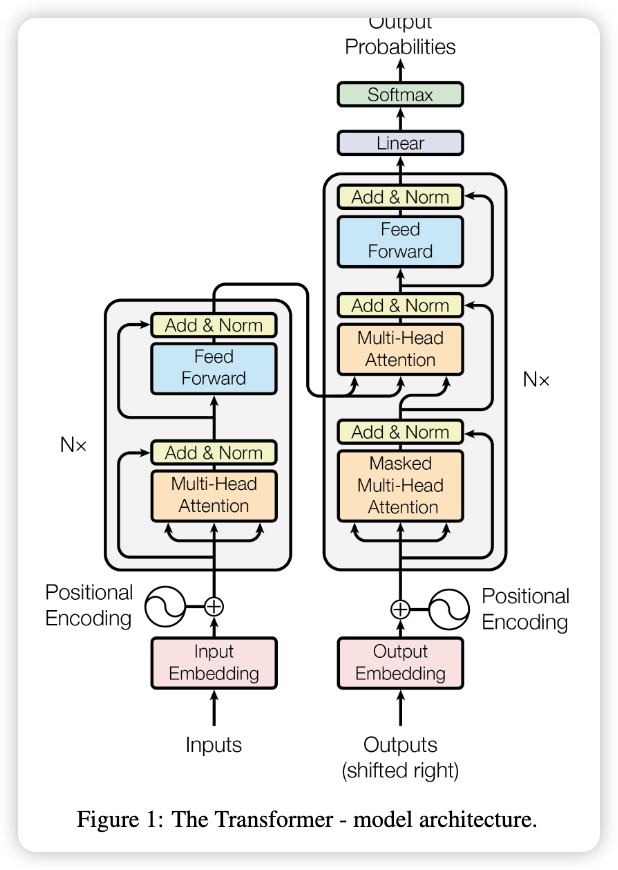
Attention is all your need

• 发表于 NeurlIPS 2017 ，引用量 17W+ 。
• Contribution：原本是应用于 翻译类 任务的，后被各种模型应用并拓展到非NLP领域。
• 主要创新点：
  • Transformer架构；
  • 多头注意力机制；
  • Encoder 与 Decoder。

BackGround

• Word2vec：

  • Embedding：

    Text representation 的目的是将非结构化数据转化为结构化数据，而其中有三种基本方法：

    1. One-hot representation | one-hot representation：一词一位
    2. Integer encoding：整数编码
    3. Word embedding：向量编码，有三种优势：(1)他可以通过低维向量来表达文本，而不是像one-hot和原字符一样长;(2)语义相近的词距离相近；(3)它用途广泛，可用于不同的任务。

  • 有两种主流的 Embedding 方法：Word2vec 和 GloVe。

  • Word2vec： 这是一种获取单词向量的统计方法。2013年，谷歌的Mikolov提出了一套新的单词嵌入方法。

    https://easyai.tech/en/ai-definition/word2vec/

    该算法有2种训练模式：

    • 通过上下文预测当前单词

    • 从当前单词中预测上下文

  • GloVe是Word2vec方法的延伸，它结合了Global statistics 和Word2vec的基于上下文的学习。

  • 与分词器(SentencePiece)区别

    项目	分词器	Word2Vec
    功能	把文本切分成词	把词转换成向量
    先后顺序	在前：得到词列表	在后：学习词向量
    是否必须	Word2Vec 需要明确的词单位进行训练，所以必须依赖分词器（尤其是中文）

Methods

Embedding

• Input Embedding 就是把自然语言转化为对应向量，此文章方法就是用Word2vec。

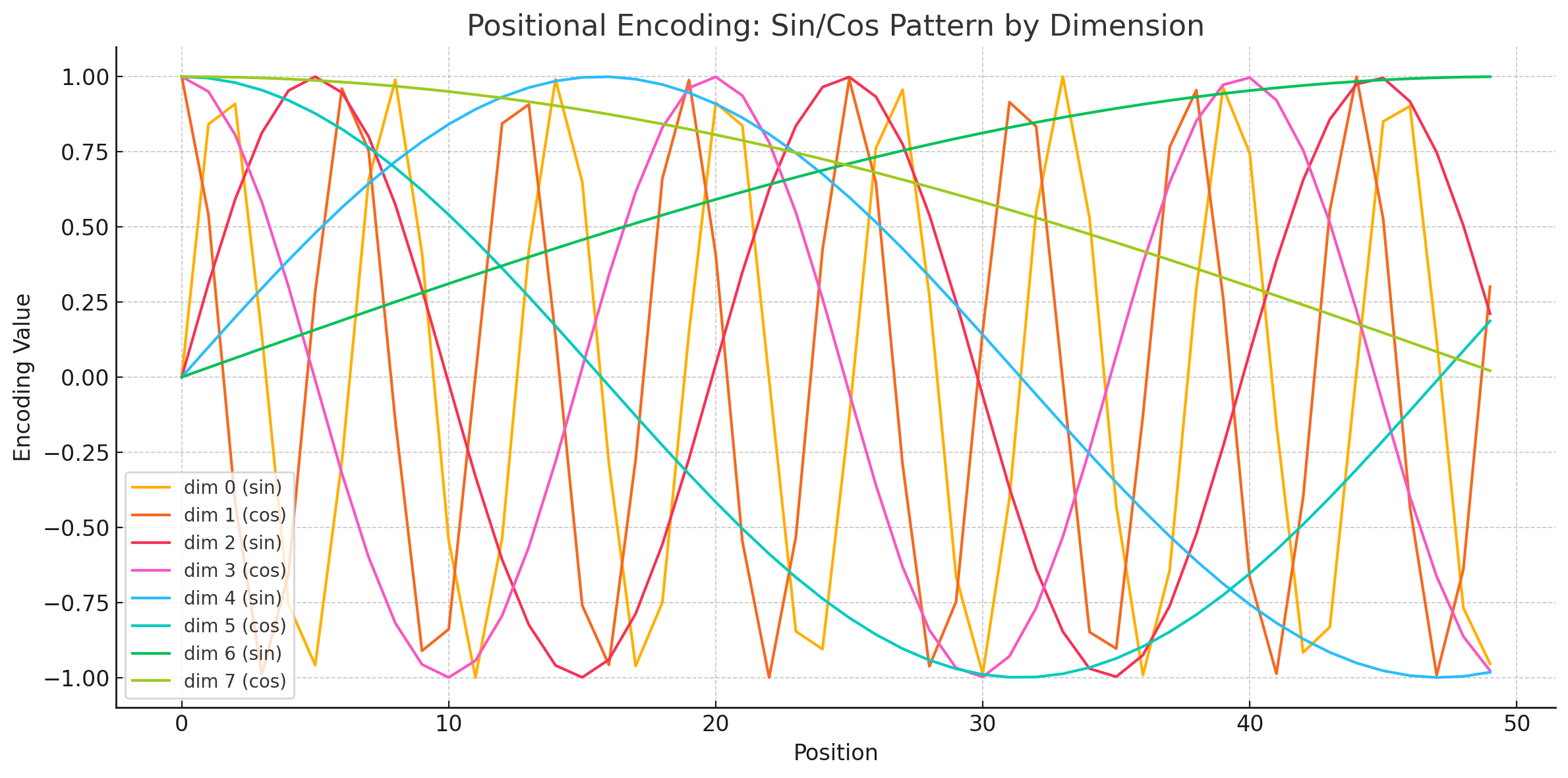
• Positional Embedding 有两种方法：1)类似于 Input Embedding，训练一个模型；2)直接用函数表示。

  2)的公示如下，纬度和Input Embedding相同，其中$pos$表示位置$i$表示纬度(也就是Input向量化后的个数)：

  $$ \begin{aligned} {P E_{( p o s, 2 i )}} & {{}=s i n ( p o s / 1 0 0 0 0^{2 i / d_{\mathrm{m o d e l}}} )} \\ {P E_{( p o s, 2 i+1 )}} & {{}=c o s ( p o s / 1 0 0 0 0^{2 i / d_{\mathrm{m o d e l}}} )} \\ \end{aligned} $$

  为什么这么设置？——可能只是为了计算方便。❌

  问题	回答
  用 sin 和 cos 是为了方便吗？	❌ 不是，它是有数学含义和表达动机的
  为什么 2i 用 sin，2i+1 用 cos？	为了引入相位差、增强表达能力、增加维度间互补性
  这种设计的好处是什么？	正交性、相位信息、多频率合成、支持相对位置推理等

  数学特征：$PE_{(pos,2i)}^2 + PE_{(pos,2i+1)}^2=1$

  好处在于：a)对于比训练长度更长的句子，例如最长为20，但是输入为21，照样可以对位置进行编码；b)容易计算出相对位置。

  不同纬度的embedding编码差异：

  

• 最终输入X：

  $$ X= Input+Postional $$

Self-Attention

The four words “with power and sum” can be highly summarized

• 核心思想就是：“从关注全部到关注重点。”

• Attention 机制最早是在计算机视觉里应用的，随后在 NLP 领域也开始应用了，真正发扬光大是在 NLP 领域，因为 2018 年 BERT 和 GPT 的效果出奇的好，进而走红。而 Transformer 和 Attention 这些核心开始被大家重点关注。

• 三大优点：参数少、速度快、效果好。

• 解决了RNN不能并行化的问题，使之不再依赖于上一步的输出。并且使长距离信息不再被弱化了，因为Attention只关注重点信息，就算文章很长，Attention也能抓住重点。

  Attention 不依赖前一步，而是：

  • 一次性拿到所有输入（如一个句子中所有词）
  • 对每个词都计算和其他所有词的相关性（打分）
  • 用这些相关性加权组合输入

  这样，所有词之间的依赖可以一起计算，就能并行了。

  ---

  🌟 举个例子

  输入句子（英文举例）： "The cat sat on the mat"

  假设我们要计算第一个词 "The" 的表示：

  Attention 会做什么？

  它会对每个词计算和 "The" 的相关性（打分），比如：

  词	相关性分数（attention score）
  The	0.1
  cat	0.3
  sat	0.2
  on	0.1
  the	0.1
  mat	0.2

  然后用这些分数对各个词的表示进行加权求和，得出 "The" 的新表示。

  ⚠️ 这里每个词的 attention 都可以同时计算，因为它们只依赖输入序列，不需要等上一个词的结果！

• Attetion的原理

  下面是使用 Encoder-Decoder 模型的机器翻译的演示。

  

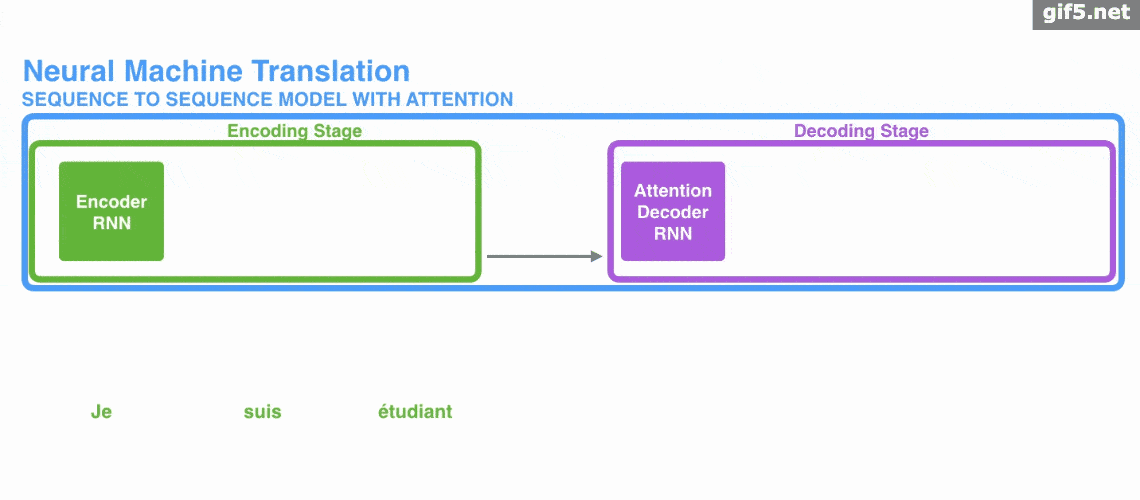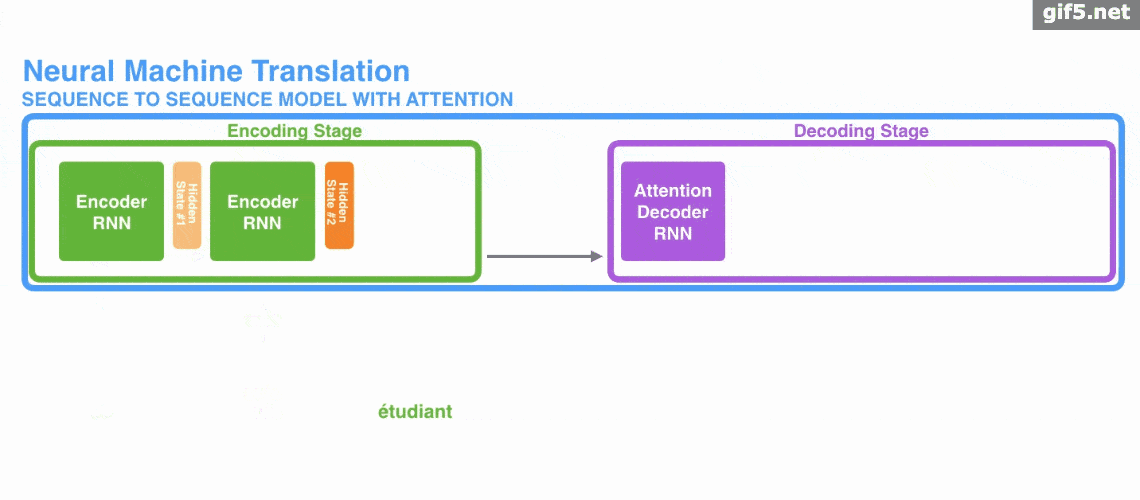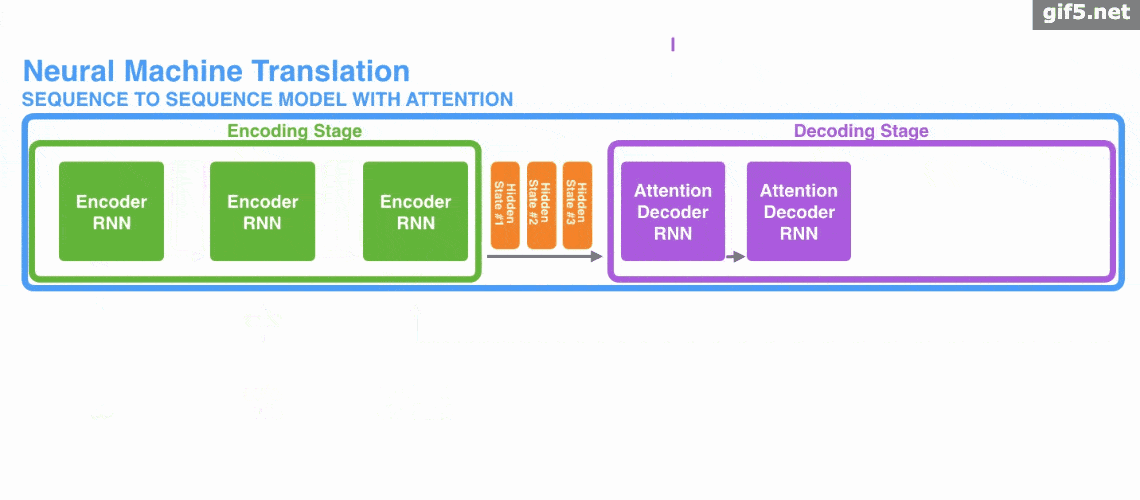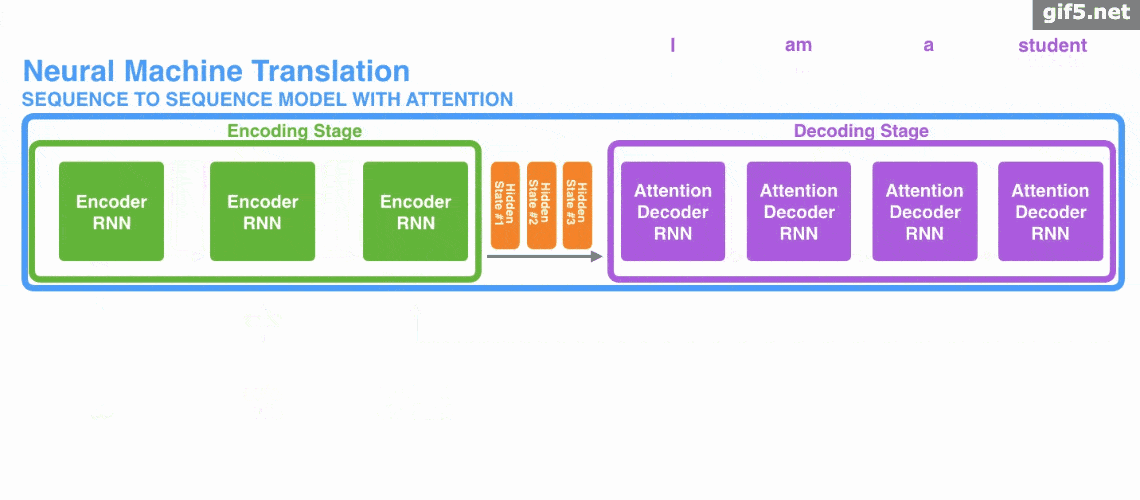
  Attention既可以应用在 Encoder-Decoder 模型中，也可以脱离其应用。

  • Attention 的三步分解

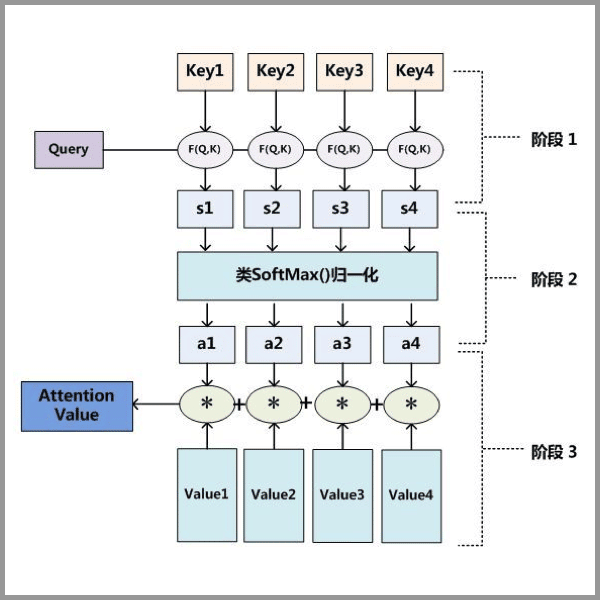    $$ \mathrm{A t t e n t i o n} ( Q, K, V )=\mathrm{s o f t m a x} \left( \frac{Q K^{T}} {\sqrt{d_{k}}} \right) V\\ Q(m,n),K(m,n),V(m,n) $$

    Step1:$Q$(query)与$K^T$(key)做矩阵乘法运算；

    Step2:归一化Step1得到的权重(weight)；

    Step3:Step2中得到的矩阵(m,m)乘$V$(Value)，得到矩阵纬度为(m,n)。

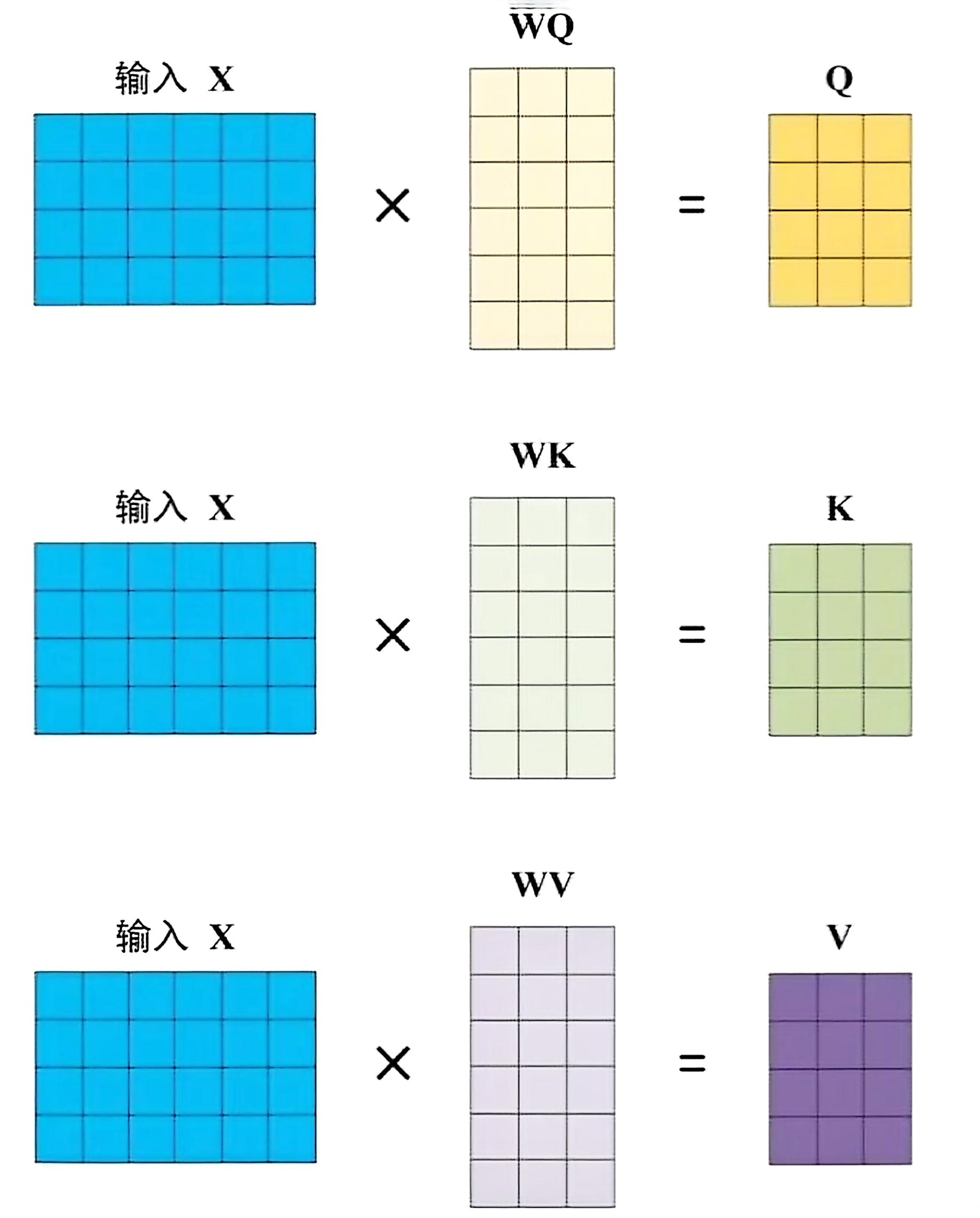
  • 解释一下上一步 $Q,K,V$ 怎么来的，是输入自然语言经过编码得到的 $X$ 转化而来的。

    

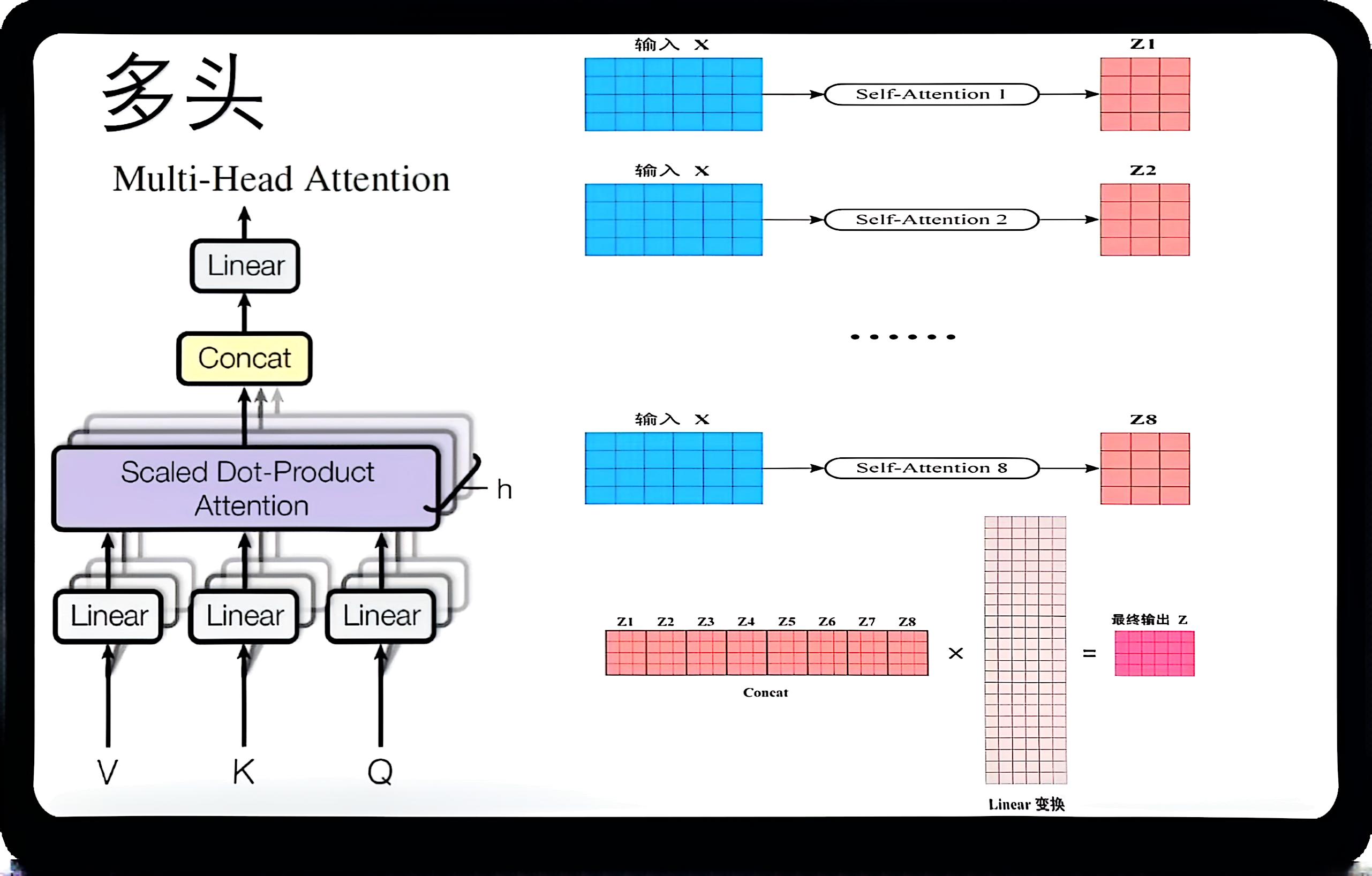
  • “多头注意力机制”中的“多头”（multi-head）是指将注意力机制拆成多个并行的子注意力机制（称为“头”），每个头都能从不同的子空间中学习信息。这种设计是 Transformer 架构中注意力机制的核心思想之一。

    $$ \begin{aligned} {{\mathrm{M u l t i H e a d}}} & {{} {{} {{} ( Q, K, V )=\mathrm{C o n c a t} ( \mathrm{h e a d}_{1},..., \mathrm{h e a d}_{h} ) W^{O}}}} \\ {{}} & {{} {{} {\mathrm{w h e r e ~ h e a d}_{i}=\mathrm{A t t e n t i o n} ( Q W_{i}^{Q}, K W_{i}^{K}, V W_{i}^{V} )}}} \\ \end{aligned} $$

    解释一下：

    传统注意力机制中，我们有一个查询向量（Query）、键向量（Key）和值向量（Value），通过这些向量计算注意力分数，然后加权求和得到结果。

    多头注意力机制的做法是：

    1. 把输入的 Query、Key、Value 各自线性变换成多个“头”，比如 8 个；
    2. 每个头用自己的 Query/Key/Value 执行一次注意力机制，得到一个输出；
    3. 把所有头的输出拼接在一起，再做一次线性变换，得到最终的输出。

    这样做的好处是：

    • 每个头可以关注输入的不同部分（比如不同位置、不同特征维度），主要体现就是前期处理的线性函数不同；
    • 增强模型表达能力，让模型可以从多个“角度”理解信息。

    形象比喻：

    可以把“多头”想象成一个人在读文章时有多个视角——比如一个视角关注人物关系，一个视角看时间线，一个视角看因果关系……最后把这些不同角度的信息整合在一起，理解更全面。

    

Add & Norm

• Add指的是 “残差连接” ，通常用于解决多层网络训练中的问题，让其只关注当前的差异部分，在ResNet中经常用到：

  $$ Add = X + MultiHead(X) $$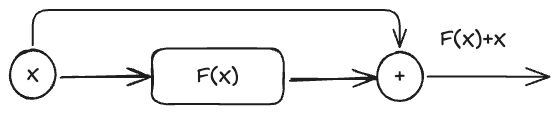

  

• Norm指的是 Layer Normaliaztion，会将每一层的输入都转化成均值方差都一样的，这样可以加快收敛。

Feed Forward

• 两层：第一层使用一个 ReLU ，第二层直接输出

  $$ FFN(x) = mac(0,xW_1+b_1)W_2 + b_2 $$

• 虽然线性转换在不同位置之间相同，但是它们使用的参数层与层之间不同。

  部分	含义
  FFN结构	两层全连接 + ReLU，中间升维再降维
  应用方式	每个位置独立处理、共享参数
  参数变化	不同层有不同参数
  计算优化角度	可以视为两个 1x1 卷积
  输入/输出维度	输入输出都是 512，中间是 2048

• 这部分还是缺乏更深刻的理解，回去找资料学习一下。

MASK

• 在输出再输入的过程中，进行MutiHeadAttention之前，需要进行一步MASK。

• 原因：翻译工作一般是顺序翻译，在翻译当前信息时只能知道前面信息而不能知道后面的。

  $$ \mathrm{A t t e n t i o n} ( Q, K, V )=\mathrm{s o f t m a x} \left( \frac{Q K^{T}M} {\sqrt{d_{k}}} \right) V\\ Q(m,n),K(m,n),V(m,n) $$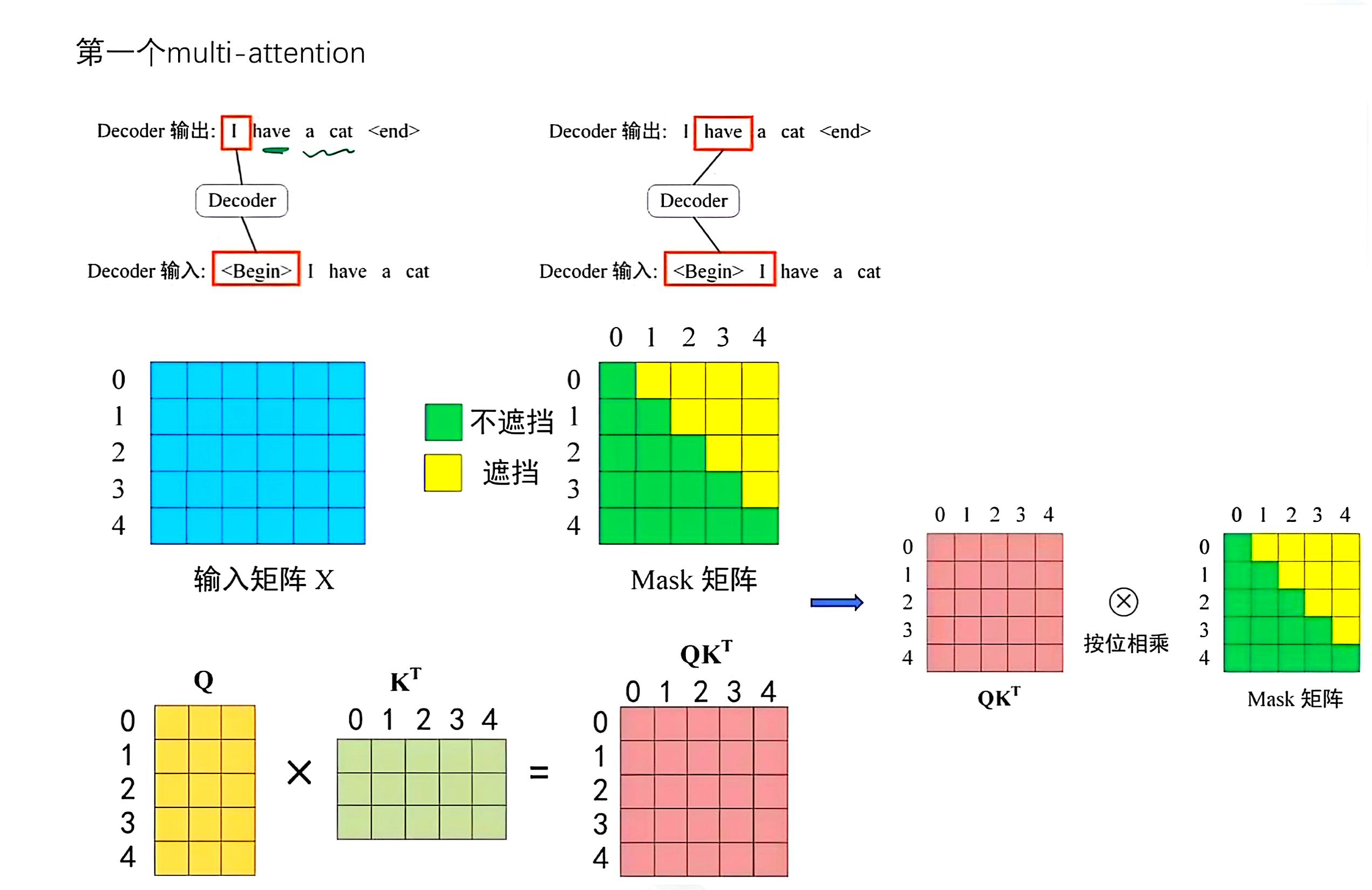

  

Decoder 结构

• 两部分输入，一个是之前的输出再输入，一个是当前输入。
• 此部分 $K,V$ 矩阵来源于 Encoder 的输出，而 $Q$ 来源于Decoder第一步分的输出。

参考资料：

• 小白也能听懂的 transformer模型原理详解 self- attention 多头注意力机制 encoder decoder 机器翻译
• Attention mechanism
• Vaswani, Ashish, et al. “Attention is all you need.” Advances in neural information processing systems 30 (2017).