LORA简介
-
Authors:$Edward Hu^* Yelong Shen^*$ 等。
-
Publication time:16 Oct 2021。
-
Motivation:使用全量参数微调模型变得难以轻易实现。
-
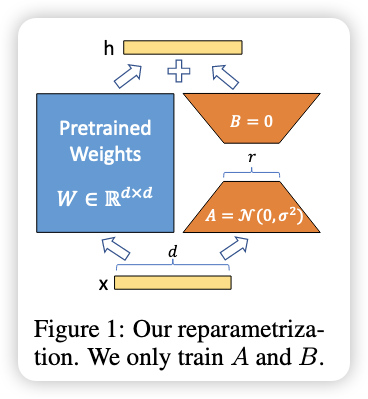
Idea:Low-Rank Adaptation(低秩适配(LoRA)):
- 冻结预训练模型的参数:大模型在预训练阶段学到的参数(也就是权重)保持不变,不再参与训练。
- 在每一层 Transformer 结构中,加入一些新的可训练矩阵:这些矩阵是“低秩分解矩阵”,也就是说它们的结构比较简单,参数很少。
- 目的是:在执行下游任务(比如文本分类、问答、翻译等)时,只需要训练这些额外添加的小矩阵,而不需要微调整个大模型。
- 好处是:大大减少了训练所需的参数量,从而节省计算资源和内存,同时还保持了模型的性能。
-
优势:
- LoRA 是轻量级插件式微调方法;
- 可以高效切换任务,只换小模块,不换大模型;
- 训练快、显存省、部署快;
- 还能和其他方法一起搭配用,不冲突。
什么是 Low-Rank?
✅ 一、从直觉上讲:
我们经常会训练神经网络里的 线性变换矩阵(比如全连接层的权重矩阵),这些矩阵可能非常大,比如 $W∈R^{d×k}$,参数量是 $d^2$。
而 低秩矩阵 的意思是:这个大矩阵其实可以被两个更小的矩阵相乘近似表示:
$W_{approx}=A⋅B$
其中:
- $A \in \mathbb{R}^{d \times r}$
- $B \in \mathbb{R}^{r \times k}$
- $r≪min(d,k)$(这个 rrr 就是“rank”,秩)
✅ 二、从 LoRA 的角度讲:
在 Transformer 中,一个典型的线性变换是:
$y = W x$
LoRA 的做法是:
-
保留原来的 WWW 不变(冻结参数)
-
在旁边加上一个 低秩可训练项:
$$ y = W x + \Delta W x \quad \text{其中} \quad \Delta W = A \cdot B $$ -
也就是说,LoRA 用了一个小的低秩矩阵 $A \cdot B$ 来对输出做一个小的“调整”,但不去动原始模型的主干参数。
✅ 三、为什么用“低秩”:
因为:
- 效率高:只需训练少量参数;
- 不易过拟合:参数少、更稳定;
- 足够灵活:即使是低秩,理论和实践都证明它可以对模型输出产生有用的改动。
Method
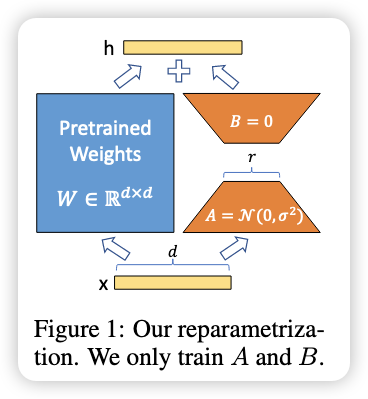
- 权重公式 $$ h=W_{0} x+\Delta W x=W_{0} x+B A x $$
-
初始化:
内容 含义 A 初始化 正态分布随机数(标准初始化) B 初始化 全 0(初始输出为 0) 输出缩放 把 $\Delta W x$ 缩放为 $\frac{\alpha}{r} \Delta W xr$ ,缩放是为了防止它影响太大或太小 目的 控制 LoRA 的干预程度、简化超参调节 实用技巧 直接设 $\alpha =$ r,无需精调,调节 $\alpha$ 就相当于调节学习率,设置与第一次尝试的 $r$ 最方便。 -
代码:https://github.com/microsoft/LoRA
参考资料:
