轻量级微调方法的粗略比较

• 方法：

  方法	全称	核心思路
  LoRA	Low-Rank Adaptation	在模型的部分权重矩阵中加入低秩可训练模块
  Adapter	Adapter Module	在模型层之间插入小型可训练模块
  Prompt Tuning	Prompt Tuning / Prefix Tuning	优化一组固定的“提示向量”来引导模型输出
  BitFit	Bias Term Fine-tuning	仅微调偏置项（bias）
  QLoRA	Quantized LoRA	在量化模型上做LoRA微调，显著节省显存
  Delta Tuning	Delta Tuning	微调某些部分（如 attention 层），而非全部参数

• 比较

  方法	训练参数	资源需求	性能	适用场景
  LoRA	少	中	高	通用任务微调
  Adapter	少	中	中高	多任务学习
  Prompt Tuning	极少	极低	中	文本生成/分类
  BitFit	极少	极低	中低	简单任务或快速试验
  QLoRA	少	低	高	大模型训练资源有限时
  Delta Tuning	少	中	中	精调注意力等模块

全量微调的主要方式和效果

• 主要方式

  类型	简述	应用方向
  标准全量微调	所有参数都参与训练	单一任务定制、预训练模型适配
  多阶段微调	先通用任务再特定任务	精细控制训练过程，提高泛化
  连续微调（Continual FT）	模型随着时间不断适应新数据	在线学习、多轮更新
  Domain-adaptive FT	预训练模型迁移到特定领域数据上	医疗、法律、金融等行业领域
  Instruction FT	使用指令数据微调模型的多样响应能力	多任务通用模型（如Alpaca、ChatGPT）

• 横向对比

  方法	训练资源	数据需求	泛化能力	应用场景
  标准全量微调	很高	中高	中	单任务、专用模型
  多阶段微调	高	高	高	多任务迁移
  持续微调	中	连续增长	中高	在线学习
  领域微调	中高	领域数据	高	医疗、法律等垂直场景
  指令微调	很高	多任务多样指令	高	通用LLM

关于FT的综述

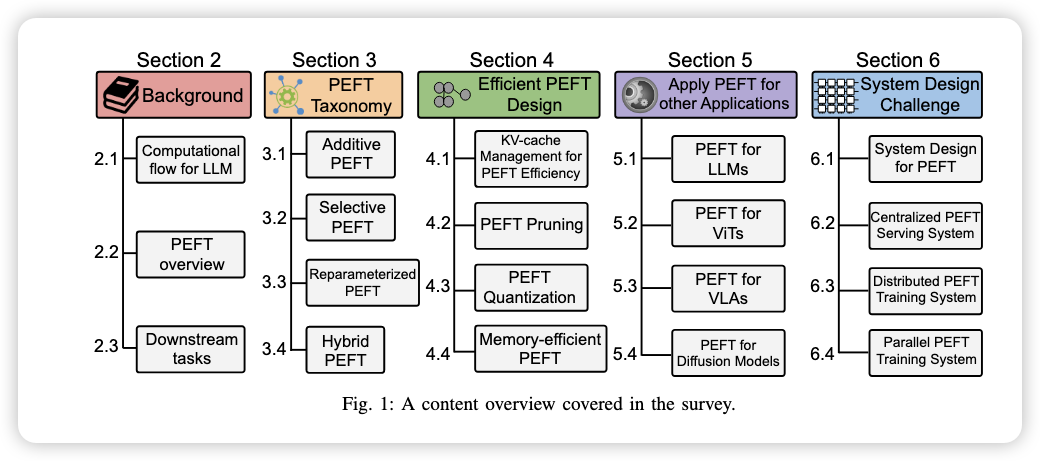
• 最新：Parameter-Efficient Fine-Tuning for Large Models: A Comprehensive Survey
• PEFT:Parameter-Efficient Fine-Tuning，指的是寻来呢大模型一小部分参数，冻结剩下的部分。
• 两个关键问题：LLM的计算流(compuatation flow)和PEFT的基本知识。
• 四种类型(三种基本类型+混合类型)：
  1. Additive algorithms：新增参数或者修改激活值，不改变原始参数？;
  2. Selective approaches：只对原始模型中的部分参数进行微调，而不是全部参数。例如选择某些层、注意力头或特定模块进行训练。;
  3. Reparamenterization PEFT：通过将模型参数转化为某种低维空间的参数表示进行训练，训练后再映射回原参数空间，从而减少训练成本且不影响推理速度。例如LoRA;
  4. Hybrid methods：上述方法的组合运用。

两个问题

• Computation flow for LLaMA

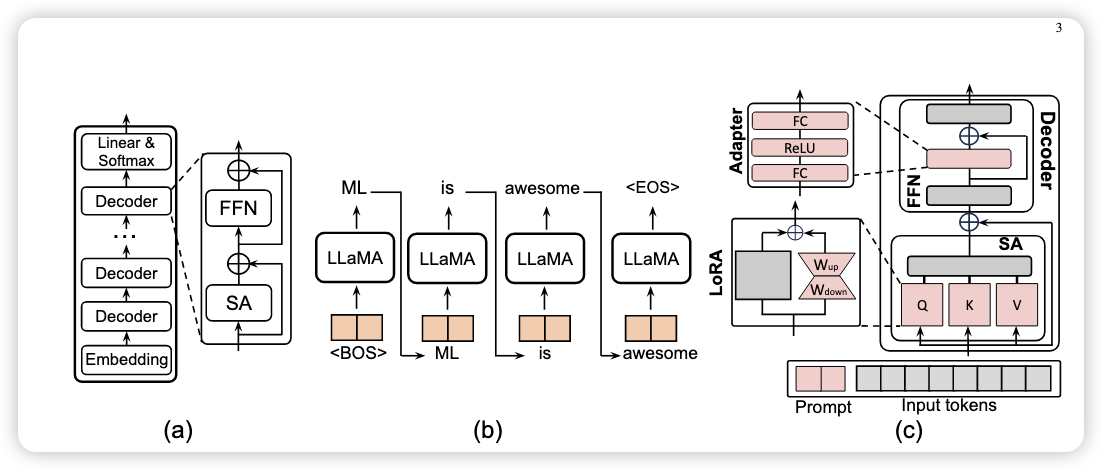
  • LLaMA 的预训练包含三个部分：Embedding block、很多 Decoder block、Head block(linear and softmax layer).

    

    • Embedding layer 作用是将自然语言文本转化为离散化向量

      Decoder layer 是由一个多头注意力机制层(Mutihead Self-Attention)和一个前馈神经网络构成(FFN)。

      输入为 $x\in R^{b \times l \times d}$ 是input token，经过三个线性转化矩阵 $W_Q,W_K,W_V$ 转化为 $query(Q),key(K),value(V)$ ，同样的，作为类Transformer模型的输入，还缺少位置编码，LLaMA使用的是(RoPE,Rotary Postional Embedding)。

    • Embedding’s MSA 层的公式：

      $$ Q,K,V = R(W_q x),R(W_k x),W_v x \\ SA(x) = Softmax(\frac{QK^T}{\sqrt{d_{head}}})V\\ MSA(x) = [SA_1(x);SA_2(x);...;SA_k(x)] $$

    • Embedding’s FFN层：

      $$ F F N_{L L a M a} ( x )=W_{u p} ( S i L U ( W_{g a t e} x ) \odot( W_{d o w n} x ) )+x $$

      另外三个权重矩阵 $W_{up},W_{down},W_{gate}$ 。使用的是SiLU激活函数($x\times \sigma(x)$)

      $$ SiLU(x)=x⋅σ(x)= \frac{x}{1+e^{-x}} $$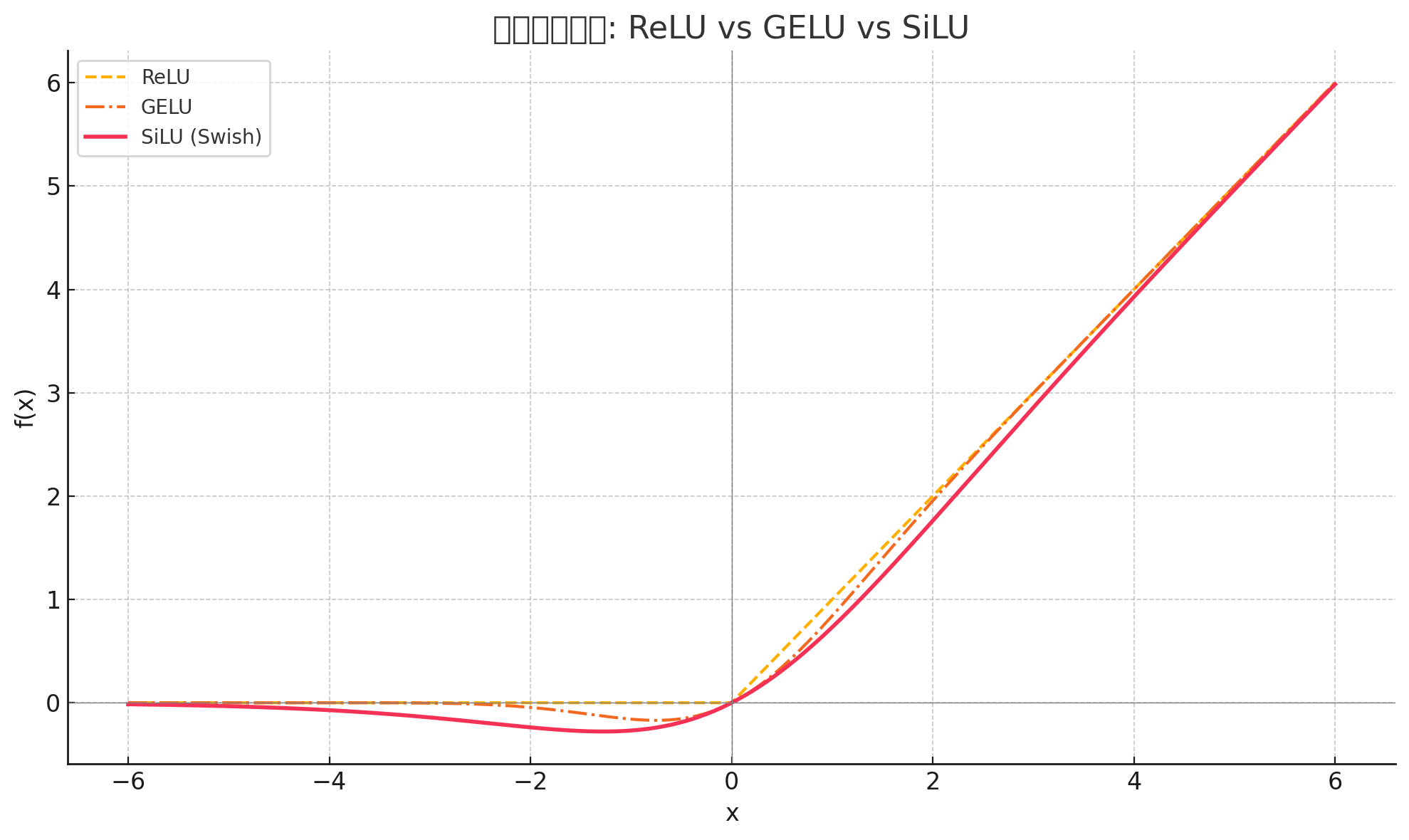

      

      为什么使用 SiLU ？

      激活函数	公式	特性	缺点
      ReLU	$max⁡(0,x)$	简单，计算高效	梯度消失（dead ReLU）问题
      GELU	$x \cdot \Phi(x)$	保留小输入信息，有较强表达能力	计算复杂，收敛速度较慢
      SiLU	$x \cdot \sigma(x)$	平滑、训练稳定、表达强	比 ReLU 慢，但比 GELU 快

    • 最后一层就是简单的线性全连接和softmax

      Linear（全连接层）

      • 作用：把 Transformer 的隐藏向量（维度比如 4096）映射到词汇表大小的向量（比如 vocab size 是 32000）。
      • 通常我们称这个为 输出投影层（output projection layer）。
      • 输出形状变为 [batch_size,seq_len,vocab_size].

      Softmax

      • 对 linear 的输出进行指数化 + 归一化，得到词汇表上每个 token 的概率分布。

      • 也就是说，softmax 的目的是：

        $$ \text{softmax}(x_i) = \frac{e^{x_i}}{\sum_j e^{x_j}} $$

  • 用于下一步做预测（如 argmax 取概率最大词）或者计算 loss（如 cross-entropy）。

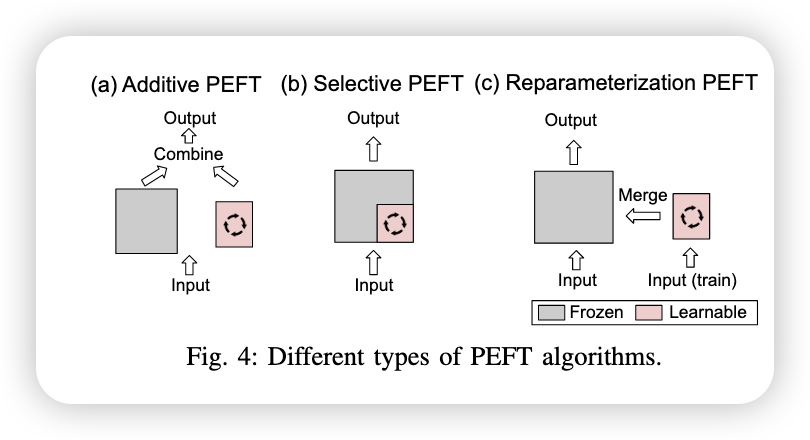
• Overview on Parameter Efficient Fine Tuning

  • additive: use additional tunable modules or parameters.
  • selective: use small subsize of parameters from the backbone model.
  • reparamenterized: use additional low-rank parameters during training ,and merge the model.
  • hybrid:

  

• LLM 评估的下游任务

  • General Language Understanding Evaluation(GLUE)：CoLA, SST-2, MRPC, STS-B, QQP, MNLI, QNLI, RTE, and WNLI
  • S
  • 促进高级提问的研究？深入了解主题和表达语言(foster research in advanced question-answering)：OpenBookQA
  • Daily scenarios：PIQA
  • Social commonsense intelligence：Social QA
  • aptly concluding sentences:HellaSwag
  • binary responses for QA: BoolQ
  • WinoGrande: 44000 problems
  • Multiple-choice: ARC-easy
  • ARC-challenge

• Evaluation Benchmarks for PEFT

  • performance, convergence, efficiency, combinability, scalability, and transferability.

    性能，收敛，效率，可组合性，可伸缩性和可传递性。

  • SharedGPT: real-world interactions with ChatGPT.focusing on the accuracy of responses and efficiency in handling requests.

  • Microsoft Azure Function Trace: the computational demands driven by events.

  • Gamma process: realistic scenarios

PEFT

1. Additive PEFT

   • 全量微调开销过大并且可能破坏LLM原有的能力

   • 冻结预训练模型并且仅引入并训练少量参数(战略性的布置参数)。大量减少存储、内存、和计算资源消耗

   • 几个典型的 Additive 算法：

     1. Adapters: 在 Transformer 块中插入 small adapter layers。

        “Adapter modules yield a compact and extensible model; they add only a few trainable parameters per task, and new tasks can be added without revisiting previous ones.”

        微调一般比基于特征的迁移(feature-based transfer)，也就是固定预训练模型参数不变，但是提取中间层的特征值，然后把特征输入新的模型中，微调表现因为参数改变要更好。

        下面是Adater的原理，整体可表示为 $ψ_{w,v}(x)$ ，其中 $w$ 冻结，训练 $v$ ，也就是下面的 Adapter 。$W_{down}$ 负责降维，$W_{up}$ 负责升维，这样可以减小训练参数量

        $$ A d a p t e r ( x )=W_{\mathrm{u p}} \sigma( W_{\mathrm{d o w n}} x )+x. $$

        σ 是非线性激活函数，如 ReLU 或 GELU

        Adapter的两个特点：a small number of parameters； a near-identity initialization(指与相较于全量模型，不然训练可能失败).

        瓶颈架构：W_up 和 W_down 分别代表降秩和升秩。

        

        ---

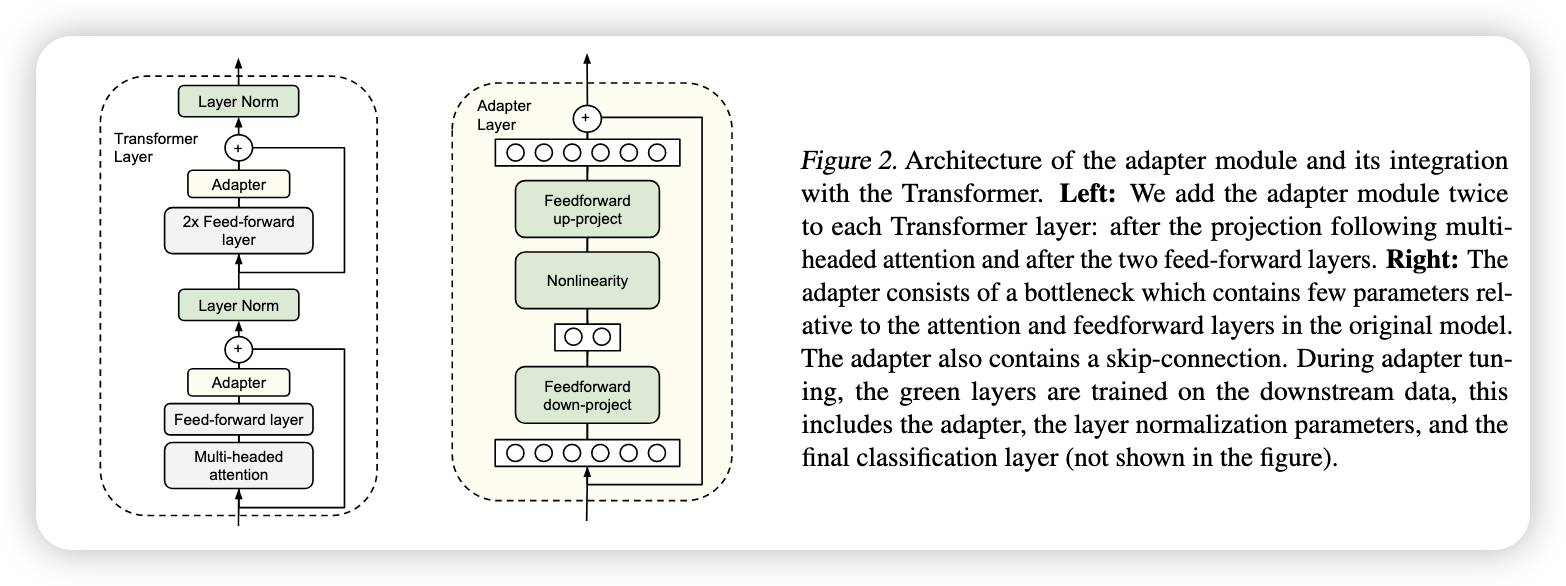
        种类

        

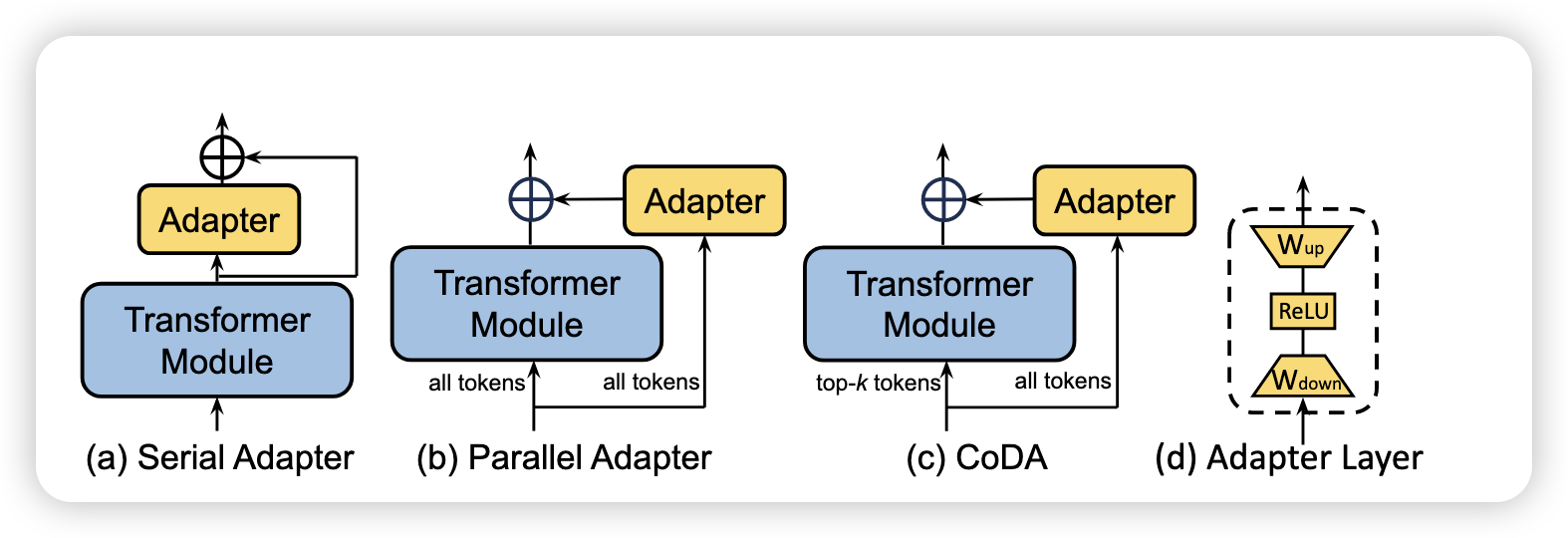
        • Serial Adapter(The first)

        • AdapterFusion: inserted only after the ’Add & Norm’ following the FFN layer to enhance efficiency.

          上述方法利用 bottlenecks 来降低参数量，但是可能减弱模型的并行性，而且需要在效率和准确率上权衡。

          即使 Transformer 的主干部分可以高度优化（如 fused attention + FFN），adapter 通常是单独模块，无法和主层融合加速。

          所以 adapter 进一步限制了层之间的并行流水线，尤其在多卡并行（Pipeline Parallelism）中表现更明显。

        • parallel adapter: use a addative adapter layers into a parallel side-network.

          CIAT，CoDA，KronA

        • CoDA: CoDA uses a soft top-k selection process that identifies k important tokens in each layer, which will be processed by both the frozen pre-trained Transformer layer and the adapter branch to maintain model accuracy.

          根据 CoDA 的设计，模型在每一层中使用 soft top-k 机制选择出最重要的 k 个 token，这些 token 会被送入冻结的预训练 Transformer 层进行处理，而所有的 token 都会经过 adapter 分支。这种设计的核心思想是：

          • 重要的 token：通过 soft top-k 机制识别，送入计算开销较大的预训练 Transformer 层，以保持模型的性能。
          • 其余的 token：仅通过计算开销较小的 adapter 分支处理，从而节省计算资源。CSDN Blog+1ar5iv+1

          这种策略使得模型能够在保持准确率的同时，实现推理速度的显著提升。实验表明，CoDA 在多个任务中相较于标准的 adapter 方法，推理速度提高了 2 到 8 倍，且准确率损失较小或没有损失。

        • multi-task learning strategies: AdapterFusion , AdaMix , PHA , AdapterSoup , MerA , and Hyperformer .

     2. Soft Prompt:

        Soft Prompt（软提示） 是一种 轻量微调（parameter-efficient tuning）方法，核心思想是：

        不改动模型本身的参数，只在输入序列前面加上一组 可学习的向量（soft prompts），来“引导”预训练模型更好地完成下游任务。

        • Prefix-tuning: introduce learnable vectors that are prepended to keys $k$ and value $v$ across all Transformer layers.

          reparameterization strategy: 使用 MLP layer 生成 prefix vectors 而不是训练 prefix。(不直接学习前缀向量本身，而是 学习一个生成前缀向量的 MLP )。

          

          🏗️ 构建方式详解

          🧩 1. 输入：Prefix Token IDs（虚拟 token）

          你首先定义一组 prefix token ids，比如长度为 10 的 prefix token。它们不是实际词汇，只是 placeholder，用于表示要插入的 prefix。

          这些 token 会被送入一个 Embedding 层，得到一个 shape 为：

          $$ \text{prefix\_embeddings} \in \mathbb{R}^{\text{prefix\_length} \times d} $$

          其中：

          • prefix_length 是 prefix token 的数量（如 10）
          • d 是隐藏层维度（例如 768）

          ---

          🔁 2. MLP：生成每层的 key 和 value 前缀向量

          然后，把这些嵌入向量送入一个 共享的 MLP（多层感知机），用于为所有 Transformer 层生成 prefix vectors。

          常见结构如下：

          1 2 3 4 5

          MLP = nn.Sequential( nn.Linear(d, hidden_dim), nn.Tanh(), nn.Linear(hidden_dim, num_layers * 2 * d) # 2 for key & value )

          输出的形状就是：

          $$ \text{prefix\_output} \in \mathbb{R}^{\text{prefix\_length} \times \text{num\_layers} \times 2 \times d}你可以 reshape 成： $$$$ \text{prefix\_kv}[l] = \{\text{key\_prefix}^{[l]}, \text{value\_prefix}^{[l]}\} \in \mathbb{R}^{\text{prefix\_length} \times d} $$

          这些就是我们要加到每一层 Transformer 的 attention 机制里的 prefix keys 和 values。

          ---

          🛠️ 3. 插入注意力机制（跨所有层）

          对于 Transformer 的每一层，在计算 Self-Attention 时：

          • 将 prefix key、value 拼接在原始 key、value 之前：

            $$ k' = \text{concat}(k_{\text{prefix}}, k_{\text{input}}) $$$$ v' = \text{concat}(v_{\text{prefix}}, v_{\text{input}}) $$

          • query 仍然是原始输入的 query。

            P-tuning v2 移除了reparameterization，并将其应用到了更大规模的NLP任务上

            APT 引入了一个自适应门机制(adaptive gate mechanism)来加强 Prefix-tuning

            p-tuning 和 prompt-tuning 将 prompt vector 只应用到了最开始的 embedding layer

            Xprompt 利用层次结构花剪枝(hierarchically structured pruning)，去除负面的token

            IDPC(InstanceDependent Prompt Generation): 使用轻量提示生成器(ligthweight prompt generating)基于每个输入句子生成提示

            LPT: 也是通过生成器生成实例感知prompt，但是这个prompt token只在中间层添加，加快了训练速率(梯度只需要计算从插入 prompt 的位置往后的部分；但是在embedding layer添加会计算整个过程的剃度)。

            • 那性能为什么还能保持甚至更好？
              • 前面层学到的是通用表示，保留它们反而避免“过拟合”；
              • prompt 作用于靠近输出的语义层，信息更集中、更有针对性；
              • 短路径反传可以更专注地调整 prompt，而不是被前面层的信息干扰。

            APrompt 除了在 key 和 value 输入加入prefix， 在 key， value， 和 query 的 self-attention 模块加入可学习的矩阵prompt，用来微调注意力。$\text{Attention}(Q, K, V) = \text{softmax}\left( \frac{QK^\top}{\sqrt{d_k}} + B \right)V$

            剩下的: SPoT, TPT, InfoPrompt, PTP, DePT, SMoP, IPT

     3. Other Additive Methods:

        • IA: 引入了三个可学习的重标定（rescaling）向量 $l_k \in R^{d_k}$ ,$l_v \in R^{d_v}$, $l_{ff}$

          $$ S A ( x )=S o f t m a x ( \frac{Q ( l_{k} \odot K^{T} )} {\sqrt{d_{h e a d}}} ) ( ( l_{v} \odot V ). $$

          In FFN, the rescaling can be denoted as:

          $$ F F N_{T r a n s f o m e r} ( x )=W_{u p} ( l_{\mathrm{f f}} \odot\sigma( W_{d o w n} x ) ), $$

        • SSF（Scale and Shift Fine-tuning） 是一种轻量级微调方法：

          • 在每个 MSA、FFN 和 LayerNorm 操作之后插入一个 SSF-ADA 层；
          • SSF-ADA 层仅做 线性缩放和偏移（scale & shift）；
          • 微调时只训练这些层，主干模型参数保持冻结；
          • 推理时这些层可以融合进原始模型参数中，不引入额外推理开销。

          它类似于 IA³，但操作更加简洁高效。

        

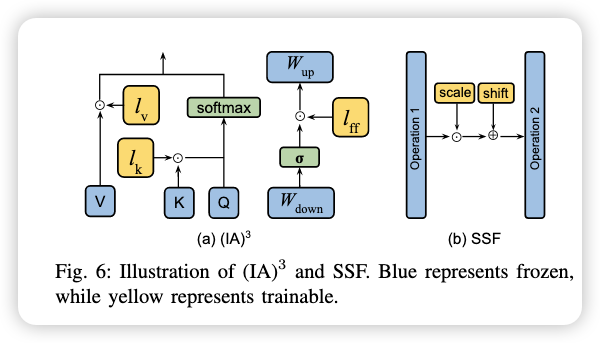
2. Select PEFT

   • 不额外训练参数，而是训练一小部分已有的参数来加强对下游任务表现。

   • 对于大小为 $n$ 的参数 $\theta = { \theta_1,\theta_2,…,\theta_n }$ ，有一个掩码 mask $M={ m_1,m_2,…,m_n }$ ， $m_i$ 是 $1\ or\ 2$ ，表示这些相关参数是否被选择用来微调。下面是参数更新公式：

     $$ \theta_{i}^{\prime}=\theta_{i}-\eta\cdot m_{i} \cdot\frac{\partial\mathcal{L}} {\partial\theta_{i}} $$

     $\eta$ 表示的是学习率

     下面是finetune的一办公式：

     $$ \operatorname* {m i n}_{\theta_{\tau}} \; \frac{1} {N} \sum_{n=1}^{N} C \left( f_{\tau} ( x_{\tau}^{( n )} ; \theta_{\tau} ), y_{\tau}^{( n )} \right)+\lambda R ( \theta_{\tau} ) $$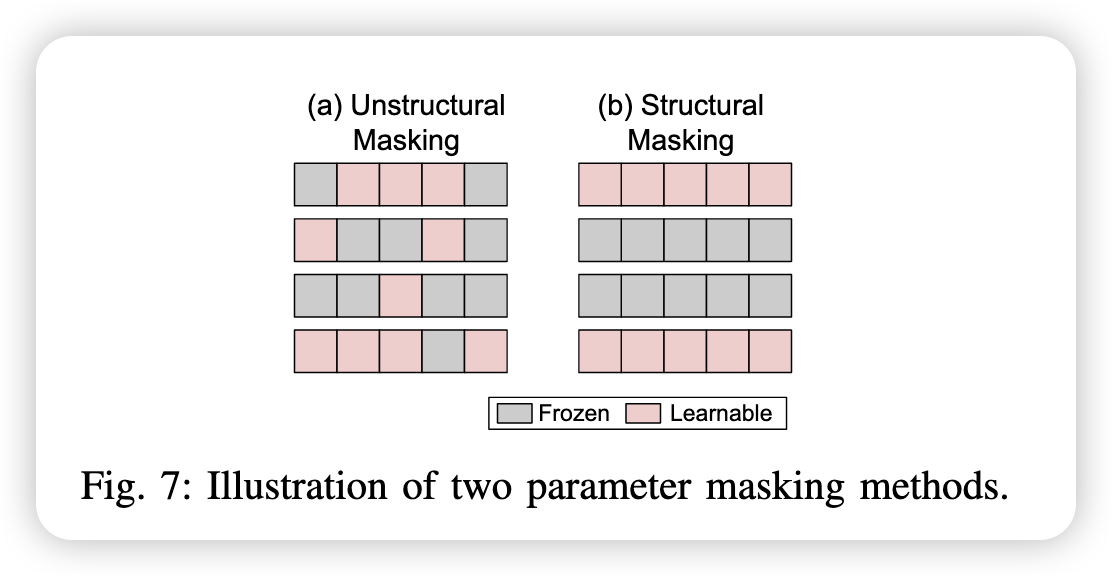

     

   • 一些具体方法：

     1. Diff Puning:

        参数公式为：$\theta_{task}=\theta_{pretrained}+\delta_{task}$ ，只训练 $\delta_{task}$ ，这个diff向量是由 $L_0-norm\ penalty$ 正则化完成的，

        which results in the following empirical risk minimization problem,

        $$ \operatorname* {m i n}_{\boldsymbol{\delta}_{\tau}} \; L ( \mathcal{D}_{\tau}, f_{\tau}, \boldsymbol{\theta}+\boldsymbol{\delta}_{\tau} )+\lambda R ( \boldsymbol{\theta}+\boldsymbol{\delta}_{\tau} ), $$

        where for brevity we define $L ( \mathcal{D}{\tau}, f{\tau}, \theta_{\tau} )$ as

        $$ L ( {\mathcal{D}}_{\tau}, f_{\tau}, \boldsymbol{\theta}_{\tau} )=\frac{1} {N} \sum_{n=1}^{N} C \left( f_{\tau} ( x_{\tau}^{( n )} ; \boldsymbol{\theta}_{\tau} ), y_{\tau}^{( n )} \right). $$

        并且使用 $L_0-norm\ penalty$ 正则化：

        $$ R ( \boldsymbol{\theta}+\boldsymbol{\delta}_{\tau} )=\| \boldsymbol{\delta}_{\tau} \|_{0}=\sum_{i=1}^{d} \mathbb{1} \{\boldsymbol{\delta}_{\tau, i} \neq0 \}. $$

        但是这个正则化式子很难优化的，因此采用Louizos et al., 2018通过“可导 mask 向量”来实现 L0 稀疏性正则化的方法,

        将 $\delta_\tau$ 转化为一个二进制的 mask 向量与一个稠密权重矩阵向量点乘:

        $$ \boldsymbol{\delta}_{\tau}=\mathbf{z}_{\tau} \odot\mathbf{w}_{\tau}, \quad\ \mathbf{z}_{\tau} \in\{0, 1 \}^{d}, \mathbf{w}_{\tau} \in\mathbb{R}^{d}. $$

        因此该问题就转化成了:

        $$ \operatorname* {m i n}_{\boldsymbol{\alpha}_{\tau}, \mathbf{w}_{\tau}} \ \mathbb{E}_{\mathbf{z}_{\tau} \sim p ( \mathbf{z}_{\tau} ; \boldsymbol{\alpha}_{\tau} )} \big[ L ( \mathcal{D}_{\tau}, f_{\tau}, \boldsymbol{\theta}+\boldsymbol{\delta}_{\tau} )+\lambda\| \boldsymbol{\delta}_{\tau} \|_{0} \big]. $$

        其中 $p(z_\tau;\alpha_\tau)$ 是由 $\alpha_\tau$ 初始化的伯努利函数。

        伯努利概率的初始化公式是：

        $$ p(z_\tau^{(i)} = 1) = \sigma(\alpha_\tau^{(i)}) = \frac{1}{1 + \exp(-\alpha_\tau^{(i)})} $$

        • $\alpha_\tau^{(i)}$ 是一个 可学习参数

        • $\sigma(\cdot)$ 是 sigmoid 函数

        • 在训练中不是直接对 $z_\tau^{(i)} \sim \text{Bernoulli}(p)$ 做采样（因为不可导）

        • 而是用 Hard Concrete Relaxation 来进行近似采样

        Hard-Concrete distribution，利用其将 $z_τ$ 被定义为样品 $u$ 与均匀分布的确定性和（子）可区分函数

        $$ \mathbf{u} \sim U ( \mathbf{0}, \mathbf{1} ), $$
        $$ {\bf s}_{\tau}=\sigma\left( \operatorname{l o g} {\bf u}-\operatorname{l o g} ( 1-{\bf u} )+\alpha_{\tau} \right), $$
        $$ \bar{\mathbf{s}}_{\tau}=\mathbf{s}_{\tau} \times( r-l )+l, $$
        $$ {\bf z}_{\tau}=\operatorname* {m i n} ( {\bf1}, \operatorname* {m a x} ( {\bf0}, \bar{\bf s}_{\tau} ) ). $$

        从而将惩罚项写成：

        $$ \mathbb{E} \left[ \left\| \boldsymbol{\delta}_{\tau} \right\|_{0} \right]=\sum_{i=1}^{d} \sigma\left( \boldsymbol{\alpha}_{\tau, i}-\operatorname{l o g} {\frac{-l} {r}} \right) $$

        最终的问题转化为求：

        $$ \operatorname* {m i n}_{\boldsymbol{\alpha}_{\tau}, \mathbf{w}_{\tau}} \mathbb{E}_{\mathbf{u} \sim U [ \mathbf{0}, \mathbf{1} ]} \left[ L ( \mathcal{D}_{\tau}, f_{\tau}, \boldsymbol{\theta}+\mathbf{z}_{\tau} \odot\mathbf{w}_{\tau} ) \right] \,+\lambda\sum_{i=1}^{d} \sigma\left( \boldsymbol{\alpha}_{\tau, i}-\operatorname{l o g} \frac{-l} {r} \right), $$

     2. 一些 Unstructural Masking:

        Diff pruning

        PaFi: 选择绝对值最小的模型训练

        FishMask: 利用近似 Fisher 信息矩阵（Fisher Information Matrix, FIM）来衡量模型参数对当前任务的重要性，从而进行“参数选择”或“参数屏蔽”。$F_i \approx \mathbb{E}_{x \sim \mathcal{D}} \left[ \left( \frac{\partial \mathcal{L}(x)}{\partial \theta_i} \right)^2 \right]$ ,此种方式就是根据任务语料进行mask选取，不能自我优化。

        Fish-Dip: 和FishMask类似的mask选择方法，但是mask可优化

        LTSFT: 选择在初始微调阶段变化最大的参数的子集以形成掩码 M

        SAM: 提出了一种二阶近似(second-order aproximation)方法，该方法通过可分析可解决的优化函数近似于原始问题，以帮助确定参数掩码。1）获取当前任务的 loss 和 gradient；2）用二阶近似计算每个参数的得分：$score_i = g_i^2 / (2 * H_{ii})$ ；3）选出 score 前 top-k 个参数；4）构造 mask m，使得只更新这些参数（其余为 0）；5）微调时只更新 mask 指定的参数。

        Child-tuning: 提出两种方式选择子网络

        但是上面的都是非结构化方法，会导致非零蒙版的分布不均匀，并在实现PEFT时降低了硬件效率。下面是一些结构化的:

        Diff-pruning: 通过将权重参数分配到本地组并将其策略性地消除，提出了一种结构化的修剪策略。

        FAR: 将FFN的权重分组到 transformer 块中，然后排序并用 $L_1$ 归一化选择。

        Bitfit: 仅微调每个DNN的偏执参数，但是大模型会失败

        S-BitFit: 应该是改良了这个方法

        Xattn Tuning: 仅微调cross-attention layers。

3. Reparameterized PEFT

   • Reparameterization(重新参数化) 代表通过转换其参数将模型的体系结构从一个变为另一个变为另一个。

   • 一般是构造一个低秩矩阵，在能够微调的同时，实现效率目标。训练好后合并，一般来说和原始的参数规模一致。

     $$ W_{\mathrm{m e r g e d}}=W_{\mathrm{b a s e}}+\alpha\cdot W_{\mathrm{L o R A}}=W_{\mathrm{b a s e}}+\alpha\cdot B A $$

   • 一些工作(Intrinsic dimensionality explains the effectiveness of language model fine-tuning)表明，模型表现出异常低的内在纬度(也就是说一个模型权重 $W_0$ 可由两个低秩矩阵相乘来表示 $A^{len \times r}B^{r\times d}$ )，

   • 最代表性工作就是 LoRA

     $$ h_{o u t}=W_{0} h_{i n}+\frac{\alpha} {r} \Delta W h_{i n}=W_{0} h_{i n}+\frac{\alpha} {r} W_{\mathrm{u p}} W_{\mathrm{d o w n}} h_{i n}, $$

     其中 $\alpha$ 表示缩放因子。在初始化时，$W_{up}$ 为高斯初始化，但是 $W_{down}$ 初始化为0矩阵，为了使初始化时模型与原模型相同。

   • 其他代表工作：

     LoRA:

     DyLORA: 解决了选择合适的秩 $r$ 的问题

     AdaLoRA: 从新计算 $\Delta W$ 为 $P \Lambda Q$ ，$\Lambda$ 为对角矩阵，里面是奇异值(singular values) $\lambda_i$ ，训练 $P, \Lambda , Q$ 三个矩阵，奇异值按照重要性分数进行修剪(which are constructed from the moving average of the magnitude of the gradient-weight product.)。其中也有惩罚项用来鼓励PQ正交 $R ( P, Q )=\left| P^{T} P-I \right|{F}^{2}+\left| Q Q^{T}-I \right|{F}^{2} $ ，这种有奇异值的LoRA也是一种调整秩大小的方式。

     SoRA: 认为AdaLoRA启发性的公式没有严谨数学证明，SoRA 没有鼓励 P 和 Q 保持正交，相反 “门” g 使用L1损失的近端梯度迭代的变化进行更新。$h_{o u t}=W_{\mathrm{u p}} ( g \odot( W_{\mathrm{d o w n}} h_{i n} ) ) $

     很多的改进型：LaplaceLoRA, LoRA Dropout, LoRA+, MoSLoRA, LoRAHub, MOELoRA

     其他非LoRA方法:

     • Compacter：

       $$ y = W_x+b\\ W = \sum_{i=1}^{n}A_i\bigotimes B_i $$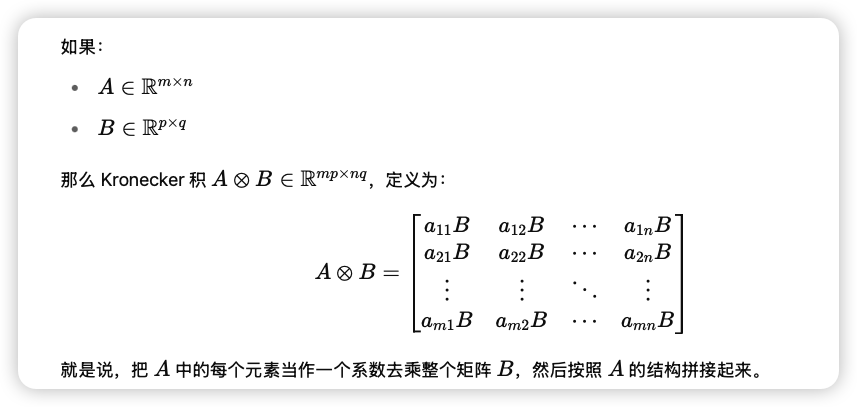

       

       两个先前工作的出的结论: 1)低层的 adpters 对结果影响不大；2)跨层共享适配器会导致某些任务的性能相对较小。

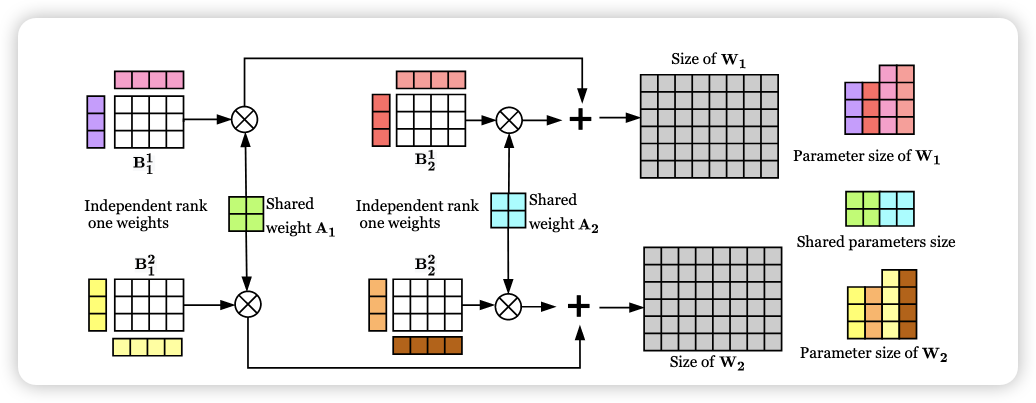
       • 在adapters之间共享参数 $A_i$ ，这些 $A_i$ 用来存储一般信息。

         

       • 对 $B_i$ 采用 low-rank subspace 技术，$B_i = s_i t_i^T$ ，其中 $s_i \in E^{\frac{k}{n} \times r}$ ,$t_i \in E^{t \times \frac{k}{n}}$

       这样最终 adapter 的 LPHM 层的权重计算式：

       $$ \boldsymbol{W} \!=\! \sum_{i=1}^{n} \boldsymbol{A}_{i} \! \otimes\! \boldsymbol{B}_{i} \!=\! \sum_{i=1}^{n} \boldsymbol{A}_{i} \! \otimes\! ( \boldsymbol{s}_{i} \boldsymbol{t}_{i}^{\top} ). $$

       Adapter层:

       $$ A^{l} ( \boldsymbol{x} ) \!=\! \mathrm{L P H M}^{U^{l}} ( \mathrm{G e L U} ( \mathrm{L P H M}^{D^{l}} ( \boldsymbol{x} ) ) ) \!+\! \boldsymbol{x} $$

     • KronA，KAdaptation也采用了Kronecker product

     • HiWi 也是在 Adapter 上改的，$W’ = W + \sigma(WW_{down})W_{up}$ ，W 应该是预训练模型的权重

     • VeRA: 采用了冻结并在层间共享的低秩矩阵 $W_{up}\ and\ W_{down} $ ，学习更小的对角矩阵 $\Lambda_b\ and\ \Lambda_d$ ，也就是：

       $$ h_{out}= W_0 h_{in} + \Lambda_b W_{up} \Lambda_d W_{down} h_{in} $$

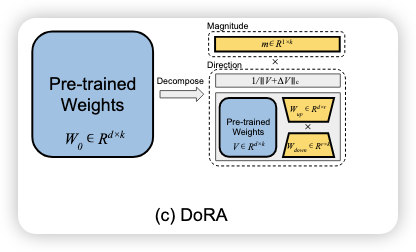
     • DoRA: 有点复杂，以后再看

       

4. Hybrid PEFT

   UniPELT: 集成了 LoRA，prefix-tuning，和adapters在transformer的每一层

   S4: 集成了多种方法，包括Adapter (A), Prefix (P), BitFit (B), and LoRA (L))

   • 四大设计原则：

     1. 分层分组：Spindle Grouping

        • 将 Transformer 的层划分为四个组 G1,G2,G3,G4G1,G2,G3,G4。

        • 每组中的层有相似的行为，因此应该使用相似的微调策略。

     2. 参数均分：Uniform Parameter Allocation

        • 微调时，在不同组之间均匀分配可训练参数数量。

     3. 全部调参：Tune All Groups

        • 四个组都需要参与调参，不跳过任何一组。

     4. 异策略分配：Different PEFTs for Different Groups

        • 在不同组中使用不同组合的 PEFT 方法，而不是统一策略。

   • 最优组合策略（在设计空间中的最佳结果）：

     分组	使用的 PEFT 方法组合
     G₁	Adapter + LoRA
     G₂	Adapter + Prefix
     G₃	Adapter + Prefix + BitFit
     G₄	Prefix + BitFit + LoRA

   MAM Adapter:

   原文:

   Parallel Adapter, which places adapter layers alongside specific layers (SA or FFN) instead of after them; Multi-head Parallel Adapter, which divides the parallel adapter into multiple heads, each affecting the head attention output in SA; and Scaled Parallel Adapter, which adds a scaling term after the parallel adapter layer, similar to LoRA.

   NOAH 和 AUTOPEFT 分别基于 AutoFormer 和贝叶斯优化算法，自动探索不同任务下最优的 PEFT 组合，显著提高了微调策略的适应性与性能，展示了 NAS 在 PEFT 优化中的强大潜力。

参考资料：Parameter-Efficient Fine-Tuning for Large Models: A Comprehensive Survey